Advertisements
Advertisements
प्रश्न
पुढील उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यापैकी अचूक उत्तराचा पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एक फासा फेकला असता नमुना अवकाशातील नमुना घटकांची संख्या ______ आहे.
विकल्प
4
6
2
52
उत्तर
एक फासा फेकला असता नमुना अवकाशातील नमुना घटकांची संख्या 6 आहे.
APPEARS IN
संबंधित प्रश्न
पुढील उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यापैकी अचूक उत्तराचा पर्याय निवडून त्याचे वर्णाक्षर लिहा.
दोन फासे फेकले असता नमुना घटकांची संख्या ______ आहे.
एक फासा टाकला असता पुढील घटनेची संभाव्यता काढण्यासाठी खालील कृती पूर्ण करा.
घटना A: वरच्या पृष्ठभागावर मूळ संख्या मिळणे.
कृती: समजा, ‘S’ नमुना अवकाश आहे.
S = {1, 2, 3, 4, 5, 6} ∴ n(S) = 6
घटना A: वरच्या पृष्ठभागावर मूळ संख्या मिळणे.
A = {______} ∴ n(A) = 3
P(A) = `square/("n"("S"))` ...........[सूत्र]
= `square/6`
∴ P(A) = `1/square`
योग्य रीतीने पिसलेल्या 52 पत्त्यांच्या कॅटमधून एक पत्ता यादृच्छिक पद्धतीने काढला, तर तो इस्पिकचा असणे या घटनेची संभाव्यता काढा.
एका खोक्यात 5 स्ट्रॉबेरीची, 6 कॉफीची व 2 पेपरमिंटची चॉकलेट्स आहेत. त्या खोक्यातील एक चॉकलेट काढले, तर खालील घटनांची संभाव्यता काढण्यासाठी कृती पूर्ण करा.
घटना A: काढलेले चॉकलेट कॉफीचे असणे.
घटना B: काढलेले चॉकलेट पेपरमिंटचे असणे.
कृती: समजा, नमुना अवकाश 'S’ आहे.
∴ n(S) = 5 + 6 + 2 = 13
घटना A : काढलेले चॉकलेट कॉफीचे असणे.
∴ n(A) = `square`
∴ P(A) = `square/("n"("S"))` ............[सूत्र]
P(A) = `square/13`
घटना B: काढलेले चॉकलेट पेपरमिंटचे असणे.
∴ n(B) = `square`
∴ P(B) = `square/("n"("S"))` ............[सूत्र]
P(B) = `square/13`
एक नाणे व एक फासा एकाचवेळी फेकले असता, पुढील घटनांची संभाव्यता काढा.
i) घटना A: काटा व सम संख्या मिळणे.
ii) घटना B: छापा व विषम संख्या मिळणे.
प्रत्येक कार्डावर एक संख्या, याप्रमाणे 1 ते 40 या संख्या लिहिलेली 40 कार्डे एका पिशवीत आहेत. त्यांपैकी एक कार्ड उचलले असता त्या कार्डावरची संख्या 5 च्या पटीत असण्याची संभाव्यता ______ असेल.
एका हॉकी संघात 6 बचाव करणारे, 4 आक्रमक व एक गोलरक्षक असे खेळाडू आहेत. यादृच्छिक पद्धतीने त्यांतील एक खेळाडू संघनायक म्हणून निवडायचा आहे, तर खालील घटनाची संभाव्यता काढा.
गोलरक्षक हा संघनायक असणे.
संधीच्या एका खेळामध्ये 1, 2, 3, 4, 5, 6, 7, 8 यांपैकी एका अंकावर बाण स्थिरावतो आणि त्या समसंभाव्य निष्पत्ती आहेत. खालील घटनांची संभाव्यता काढा.
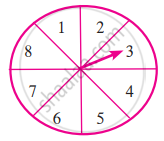
- तो बाण 8 या अंकावर स्थिरावणे.
- तो बाण विषम अंकावर स्थिरावणे.
- बाणाने दर्शवलेली संख्या 2 पेक्षा मोठी असणे.
- बाणाने दर्शवलेली संख्या 9 पेक्षा लहान असणे.
एका फाशाच्या पृष्ठभागावर 0, 1, 2, 3, 4, 5 या संख्या आहेत. हा फासा दोनदा फेकला, तर वरच्या पृष्ठांवर मिळालेल्या संख्यांचा गुणाकार शून्य असण्याची संभाव्यता काढा.
एक फासा टाकला असता वरच्या पृष्ठभागावर मूळ संख्या मिळण्याची संभाव्यता काढण्याची कृती पूर्ण करून लिहा.
कृती:
एक फासा टाकला असता नमुना अवकाश 'S' आहे.
S = `{square}`
∴ n(S) = 6
घटना A: वरच्या पृष्ठभागावर मूळ संख्या मिळणे.
A = `{square}`
∴ n(A) = 3
∴ P(A) = `square/("n"("S"))` ............(सूत्र)
∴ P(A) = `square`
