Advertisements
Advertisements
प्रश्न
Resolve the following rational expressions into partial fractions
`(2x^2 + 5x - 11)/(x^2 + 2x - 3)`
उत्तर
`(2x^2 + 5x - 11)/(x^2 + 2x - 3)`
Since the degree of the numerator is equal to the degree of the denominator divide the numerator by the denominator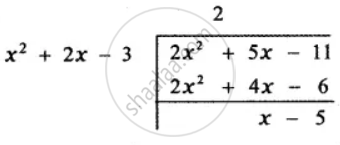
`(2x^2 + 5x - 11)/(x^2 + 2x - 3) = 2 + (x - 5)/(x^2 + 2x - 3)` ......(1)
Consider `(x - 5)/(x^2 + 2x - 3)`
`(x - 5)/(x^2 + 2x - 3) = (x - 5)/(x^2 + 3x - x - 3)`
= `(x - 5)/(x(x + 3) - 1(x + 3))`
`(x - 5)/(x^2 + 2x - 3) = (x - 5)/((x - 1) (x + 3))`
`(x - 5)/(x^2 + 2x - 3) = "A"/(x - 1) + "B"/(x + 3)` ......(2)
`(x - 5)/(x^2 + 2x - 3) = ("A"(x + 3) + "B"(x - 1))/((x - 1) (x + 3))`
x – 5 = A(x + 3) + B(x – 1) ......(3)
Put x = 1 in equation (3)
1 – 5 = A(1 + 3) + B(1 – 1)
– 4 = 4A + 0
⇒ A = – 1
Put x = – 3 in equation (3)
– 3 – 5 = A(– 3 + 3) + B(– 3 – 1)
– 8 = 0 – 4B
⇒ B = 2
Substituting the values of A and B in equation (2) we have
`(x - 5)/(x^2 + 2x - 3) = (-1)/(x - 1) + 2/(x + 3)`
∴ The required partial fraction is
`(2x^2 + 5x - 11)/(x^2 + 2x - 3) = 2 + 2/(x + 3) - 1/(x - 1)`
APPEARS IN
संबंधित प्रश्न
Find all values of x that satisfies the inequality `(2x - 3)/((x - 2)(x - 4)) < 0`
Resolve the following rational expressions into partial fractions
`1/(x^2 - "a"^2)`
Resolve the following rational expressions into partial fractions
`(3x + 1)/((x - 2)(x + 1))`
Resolve the following rational expressions into partial fractions
`x/((x^2 + 1)(x - 1)(x + 2))`
Resolve the following rational expressions into partial fractions
`x/((x - 1)^3`
Resolve the following rational expressions into partial fractions
`1/(x^4 - 1)`
Resolve the following rational expressions into partial fractions
`(x - 1)^2/(x^3 + x)`
Resolve the following rational expressions into partial fractions
`(x^2 + x + 1)/(x^2 - 5x + 6)`
Resolve the following rational expressions into partial fractions
`(6x^2 - x + 1)/(x^3 + x^2 + x + 1)`
Determine the region in the plane determined by the inequalities:
x ≤ 3y, x ≥ y
Determine the region in the plane determined by the inequalities:
y ≥ 2x, −2x + 3y ≤ 6
Determine the region in the plane determined by the inequalities:
3x + 5y ≥ 45, x ≥ 0, y ≥ 0
Determine the region in the plane determined by the inequalities:
2x + 3y ≤ 35, y ≥ 2, x ≥ 5.
Determine the region in the plane determined by the inequalities:
2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0
Determine the region in the plane determined by the inequalities:
x − 2y ≥ 0, 2x − y ≤ −2, x ≥ 0, y ≥ 0
Determine the region in the plane determined by the inequalities:
2x + y ≥ 8, x + 2y ≥ 8, x + y ≤ 6
Choose the correct alternative:
The solution of 5x − 1 < 24 and 5x + 1 > −24 is
Choose the correct alternative:
The solution set of the following inequality |x − 1| ≥ |x − 3| is
