Advertisements
Advertisements
प्रश्न
शांति स्वीट स्टाल अपनी मिठाइयों को पैक करने के लिए गत्ते के डिब्बे बनाने का ऑर्डर दे रहा था। दो मापों के डिब्बों की आवश्यकता थी। बड़े डिब्बों की माप 25 सेमी X 20 सेमी X 5 सेमी और छोटे डिब्बे की माप 15 सेमी X 12 सेमी X 5 सेमी थीं। सभी प्रकार की अतिव्यापिकता (Over Laps) के लिए कुल पृष्ठीय क्षेत्रफल के 5% के बराबर अतिरिक्त गत्ता लगेगा। यदि गत्ते की लागत ₹ 4 प्रति 1000 सेमी2 है, तो प्रत्येक प्रकार के 250 डिब्बे बनवाने की कितनी लागत आएगी?
Advertisements
उत्तर
बड़े डिब्बे की लंबाई (l1) = 25 सेमी
बड़े डिब्बे की चौड़ाई (b1) = 20 cm
बड़े डिब्बे की ऊँचाई (h1) = 5 cm
बड़े बॉक्स का कुल पृष्ठीय क्षेत्रफल = 2(lb + lh + bh)
= [2 (25 × 20 + 25 × 5 + 20 × 5)] सेमी2
= [2(500 + 125 + 100)] सेमी2
= 1450 सेमी2
`"ओवरलैपिंग के लिए आवश्यक अतिरिक्त क्षेत्र"= ((1450xx5)/100)cm^2 = 72.5 cm^2`
सभी ओवरलैप पर विचार करते हुए, 1 बड़े बॉक्स का कुल सतह क्षेत्र
= (1450 + 72.5) सेमी2 =1522.5 सेमी2
ऐसे 250 बड़े बक्सों के लिए आवश्यक कार्डबोर्ड शीट का क्षेत्रफल
= (1522.5 × 250) सेमी2 = 380625 सेमी2
इसी प्रकार, छोटे डिब्बे का कुल पृष्ठीय क्षेत्रफल = [2(15 × 12 + 15 × 5 + 12 × 5] सेमी2
= [2(180 + 75 + 60)] सेमी2
= (2 × 315) सेमी2
= 630 सेमी2
`"इसलिए, अतिव्यापी के लिए आवश्यक अतिरिक्त क्षेत्र"= ((630xx5)/100)cm^2 = 31.5cm^2`
सभी ओवरलैप पर विचार करते हुए 1 छोटे बॉक्स का कुल सतह क्षेत्र
= (630 + 31.5) सेमी2 = 661.5 सेमी2
250 छोटे बक्सों के लिए आवश्यक कार्डबोर्ड शीट का क्षेत्रफल = (250 × 661.5) सेमी2
= 165375 सेमी2
कुल कार्डबोर्ड शीट की आवश्यकता = (380625 + 165375) सेमी2
= 546000 सेमी2
1000 सेमी2 कार्डबोर्ड शीट की कीमत = रु 4
546000 सेमी2 कार्डबोर्ड शीट की कीमत `=((546000xx4)/1000) = "रु. "2184`
अत: ऐसे प्रत्येक प्रकार के 250 ऐसे बक्सों के लिए आवश्यक कार्डबोर्ड शीट की कीमत 2184 रुपये होगी।
संबंधित प्रश्न
एक छोटा पौधा घर (Green House) सम्पूर्ण रूप से शीशे की पट्टियों से (आधार भी सम्मिलित है) घर के अंदर ही बनाया गया है और शीशे की पट्टियों को टेप द्वारा चिपका कर रोका गया है। यह पौधा घर 30 सेमी लम्बा, 25 सेमी चौड़ा और 25 सेमी ऊँचा है।
इसमें प्रयुक्त शीशे की पट्टियों का क्षेत्रफल क्या है?
परवीन अपनी कार खड़ी करने के लिए, एक संदूक के आकार के ढाँचे जैसा एक अस्थाई स्थान तिरपाल की सहायता से बनाना चाहती है, जो कार को चारों ओर से और ऊपर से ढक ले (सामने वाला फलक लटका हुआ होगा जिसे घुमाकर ऊपर किया जा सकता है)। यह मानते हुए कि सिलाई के समय लगा तिरपाल का अतिरिक्त कपड़ा नगण्य होगा, आधार विमाओं 4 मीटर X 3 मीटर और ऊँचाई 2.5 मीटर वाले इस ढांचे को बनाने के लिए कितने तिरपाल की आवश्यकता होगी?
एक रोलर (Roller) का व्यास 84 सेमी है और लंबाई 120 सेमी है। एक खेल के मैदान को एक बार समतल करने के लिए 500 चक्कर लगाने पड़ते हैं। खेल के मैदान का मी2 में क्षेत्रफल ज्ञात कीजिए।
`["मान लें "pi=22/7]`
एक लम्ब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 4.4 मी2 है। यदि बेलन के आधार की त्रिज्या 0.7 मी है, तो उसकी ऊँचाई ज्ञात कीजिए।
`["मान लें "pi=22/7]`
एक ऐसे घन की भुजा ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 600 cm2 है।
रुखसार ने 1 m × 2 m × 1.5 m माप वाली एक पेटी को बाहर से पेंट किया। यदि उसने पेटी के तल के अतिरिक्त उसे सभी जगह से पेंट किया हो तो ज्ञात कीजिए कि उसने कितने पृष्ठीय क्षेत्रफल को पेंट किया।
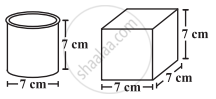
वर्णन कीजिए कि दाईं तरफ की गई आकृतियाँ किस प्रकार एक समान हैं और किस प्रकार एक दूसरे से भिन्न हैं? किस डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल अधिक है?
किसी समघन की भुजा 4.5 सेमी हो, तो उस समघन के उर्ध्वाधर पृष्ठों का क्षेत्रफल तथा संपूर्ण पृष्ठफल ज्ञात कीजिए।
किसी समघन का संपूर्ण पृष्ठफल 5400 वर्ग सेमी है तो उस समघन की उर्ध्वाधर पृष्ठों का क्षेत्रफल ज्ञात कीजिए।
किसी घन के संपूर्ण पृष्ठफल 864 वर्ग सेमी है तो उसका घनफल ज्ञात कीजिए।
