Question

Show that the length of curve `9ay^2=x(x-3a)^2  "is"  4sqrt3a`

Answer 1

Curve : `9ay^2=x(x-3a)^2` ................(1)
The given curve is strophoid.

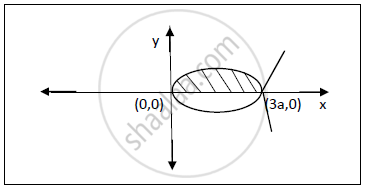
Differentiate eqn (1) w.r.t x,

`18ay(dy)/(dx)=2x(x-3a)+(x-3a)^2`

`18ay(dy)/(dx)=2x(x-3a)+(x-3a)^2`

`therefore(dy)/(dx)=((x-3a)(x-a))/(6ay)`

Squaring both the sides,

`((dy)/(dx))^2=((x-3a)^2(x-a)^2)/(36a^2y^2)`

`therefore((dy)/(dx))^2=((x-3a)^2(x-a)^2)/(4ax(x-3a)^2)` ............from(1)

`therefore((dy)/(dx))^2=(x-a)^2/(4ax)`

The perimeter of given curve is ,

`S=int_0^(3a)sqrt(1+((dy)/(dx))^2dx)=int_0^(3a)sqrt(1+(x-a)^2/(4ax))dx=int_0^(3a)sqrt((x+a)^2/(4ax))dx`

`therefore S=int_0^(3a) (x+a)/(2sqrtxsqrta)dx`

`therefore S=1/(2sqrta)int_0^(3a) (x+a)/sqrtxdx`

`=1/(2sqrta)[(2xsqrtx)/3+2sqrtx]_0^(3a)`

`=1/(2sqrta)[(2asqrt(3a))/1+2sqrt3a]`

`thereforeS=2sqrt3`  ......................( Half curve length)

∴ The total length of given curve = 2 S = 4`sqrt3` units.