Advertisements
Advertisements
प्रश्न
Simplify:
उत्तर
\[\frac{7}{9} + \frac{3}{- 4} = \frac{7}{9} + \frac{- 3}{4}\]
\[\text{L.C.M. of thedenominators 9 and 4 is 36}.\]
\[\text{Now, we willexpress}\frac{7}{9}\text{and}\frac{- 3}{4}\text{in the form in which they take thedenominator 36.}\]
\[\frac{7 \times 4}{9 \times 4} = \frac{28}{36}\]
\[\frac{- 3 \times 9}{4 \times 9} = \frac{- 27}{36}\]
\[\text{So}\]
\[\frac{7}{9} + \frac{- 3}{4} = \frac{28}{36} + \frac{- 27}{36}\]
\[ = \frac{28 + ( - 27)}{36}\]
\[ = \frac{28 - 27}{36}\]
\[ = \frac{1}{36}\]
APPEARS IN
संबंधित प्रश्न
The sum of the two numbers is \[\frac{5}{9} .\] If one of the numbers is \[\frac{1}{3},\] find the other.
Divide:
Find ten rational numbers between \[\frac{1}{4} \text{and} \frac{1}{2} .\]
For each set of rational number, given below, verify the associative property of addition of rational number:
(ii) `(-2)/5, 4/15 and (-7)/10`
Compare: `- 3 "and" 2 3/4 or 11/4`
Insert a rational number between:
101 and 102
Insert five rational number between:
`(2)/(5) and (2)/(3)`
0 is whole number but it is not a rational number.
The diagram shows the wingspans of different species of birds. Use the diagram to answer the question given below:
| Golden eagle | Blue jay |
 |
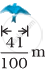 |
How much longer is the wingspan of a Golden eagle than the wingspan of a Blue jay?
In a rational number, denominator always has to be a non-zero integer.
