Advertisements
Advertisements
प्रश्न
समकोण Δ LMN में, ∠ N =θ, ∠M = 90°, cos θ =`24/25` तो sin θ तथा tan θ इस अनुपात का मान ज्ञात कीजिए। इसी प्रकार sin2 θ तथा cos2 θ का मान ज्ञात कीजिए।

उत्तर

समकोण Δ LMN में, ∠N = θ.
cos θ = `24/25`
⇒ `"MN"/"LN" = 24/25`
Let MN = 24k और LN = 25k.
पाइथागोरस प्रमेय का उपयोग करते हुए,
LN2 = LM2 + MN2
⇒ (25k)2 = LM2 + (24k)2
⇒ LM2 = 625k2 − 576k2 = 49k2
⇒ LM2 = (7k)2
⇒ LM = 7k
sin θ = `["LM"]/["LN"] = [7k]/[25k] = 7/25`
tan θ = `["LM"]/["NM"] = [7k]/[24k] = 7/24`
sin2 θ = `( 7/25)^2 = 49/625`
cos2 θ = `(24/25)^2 = 576/625`
APPEARS IN
संबंधित प्रश्न
संलग्न आकृति में Δ PQR का ∠R यह समकोण है तो निम्नलिखित अनुपात लिखिए।
- sin P
- cos Q
- tan P
- tan Q

आकृति में `triangle`XYZ यह समकोण त्रिभुज है। `angle`XYZ = 90° है। भुजा की लंबाई क्रमशः a,b,c इस प्रकार दी गई है। इस आधार पर निम्नलिखित अनुपात लिखिए।
- sin X
- tan Z
- cos X
- tan X

समकोण `triangle` LMN में, `angle`LMN = 90° `angle`L = 50° तथा `angle`N = 40° है। इस आधार पर निम्नलिखित अनुपात लिखिए।
- sin 50°
- cos 50°
- tan 40°
- cos 40°

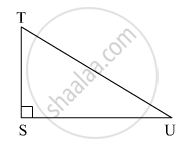
समकोण Δ TSU में TS = 5, ∠S = 90°, SU = 12 तो sin T, cos T, tan T का मान ज्ञात कीजिए। इसी प्रकार sin U, cos U, tan U का भी मान ज्ञात कीजिए।
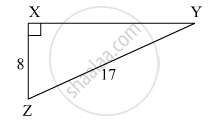
समकोण ΔYXZ में, ∠ X = 90°, XZ = 8 सेमी, YZ = 17 सेमी, तो sin Y, cos Y, tan Y, sin Z, cos Z, tan Z का मान ज्ञात कीजिए।