Advertisements
Advertisements
प्रश्न
Solve the following simultaneous equations: `7/(2X+1)+13/(Y+2)=27,13/(2X+1)+7/(Y+2)=33`
उत्तर
`7/(2x+1)+13/(y+2)=27` .........(1)
`13/(2x+1)+7/(y+2)=33` ...........(2)
Substituting`1/(2x+1)=m` and`1/(y+2)=n` in equations (1) and (2), we get
7m+13n=27 .............(3)
and 13m+7n=33 ..........(4)
Adding equations (3) and (4), we get
20m+20n=60
∴m+n=3 ...............(5)
Subtracting equation (3) from equation (4), we get
6m-6n=6
∴m-n= 1 ...........(6)
Adding equations (5) and (6), we get
2m= 4
∴ m= 2
Substituting m = 2 in equation (5), we get
2 - n= 1
∴ n = 1
Resubstituting the values of m and n, we get
`1/(2x+1)=m= 2`
⇒ 2x + 1=`1/2`
⇒ x = `(-1)/4`
and `1/(y+2)=n =1`
⇒ y +2 =1
⇒ y = -1
∴ x=`(-1)/4` and y= -1.
संबंधित प्रश्न
Solve the following system of equations `\frac { 1 }{ 2x } – \frac { 1 }{ y } = – 1; \frac { 1 }{ x } + \frac { 1}{ 2y } = 8`
Solve the following pairs of equations by reducing them to a pair of linear equations
`1/(2x) + 1/(3y) = 2`
`1/(3x) + 1/(2y) = 13/6`
Solve the following pairs of equations by reducing them to a pair of linear equations
`5/(x-1) + 1/y-2 = 2`
`6/(x-1) - 3/(y-2) = 1`
Formulate the following problems as a pair of equations, and hence find their solutions:
Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current
Formulate the following problems as a pair of equations, and hence find their solutions:
Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
One says, "Give me a hundred, friend! I shall then become twice as rich as you". The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital? [From the Bijaganita of Bhaskara II)
[Hint: x + 100 = 2 (y − 100), y + 10 = 6(x − 10)]
A train covered a certain distance at a uniform speed. If the train would have been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
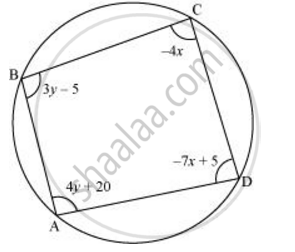
ABCD is a cyclic quadrilateral finds the angles of the cyclic quadrilateral.
Find the value of following determinant.
`|(-1,7),(2,4)|`
Find the value of following determinant.
`|(5,3), (-7,0)|`
Find the values of following determinant.
`|(7/3,5/3), (3/2, 1/2)|`
The sum of two numbers is 8. If their sum is four times their difference, find the numbers.
A two-digit number is 4 more than 6 times the sum of its digits. If 18 is subtracted from the number, the digits are reversed. Find the number.
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If the numerator is multiplied by 2 and the denominator is reduced by 5, the fraction becomes `6/5`. Thus, we have
`(2x)/(y-5)=6/5`
`⇒ 10x=6(y-5)`
`⇒ 10x=6y-30`
`⇒ 10x-6y+30 =0`
`⇒ 2(5x-3y+15)=0`
`⇒ 5x - 3y+15=0`
If the denominator is doubled and the numerator is increased by 8, the fraction becomes `2/5`. Thus, we have
`(x+8)/(2y)=2/5`
`⇒ 5(x+8)=4y`
`⇒ 5x+40=4y`
`⇒ 5x-4y+40=0`
So, we have two equations
`5x-3y+15=0`
`5x-4y+40=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-3)xx40-(-4)xx15)=-y/(5xx40-5xx15)=1/(5xx(-4)-5xx(-3))`
`⇒ x/(-120+60)=(-y)/(200-75)=1/(-20+15)`
`⇒x/(-60)=-y/125``=1/-5`
`⇒ x= 60/5,y=125/5`
`⇒ x=12,y=25`
Hence, the fraction is `12/25`
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If 3 is added to the denominator and 2 is subtracted from the numerator, the fraction becomes `1/4`. Thus, we have
`(x-2)/(y+3)=1/4`
`⇒ 4(x-2)=y+3`
`⇒ 4x-8=y+3`
`⇒ 4x-y-11=0`
If 6 is added to the numerator and the denominator is multiplied by 3, the fraction becomes `2/3`. Thus, we have
`(x+6)/(3y)=2/3`
`⇒ 3(x+6)=6y`
`⇒ 3x +18 =6y`
`⇒ 3x-6y+18=0`
`⇒ 3(x-2y+6)=0`
`⇒ x-3y+6=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-1)xx6-(-2)xx(-11))=(-y)/(4xx6-1xx(-11))=1/(4xx(-2)-1xx(-1))`
`⇒ x/(-6-22)=-y/(24+11)=1/(-8+1)`
`⇒ x/-28=-y/35=1/-7`
`⇒ x= 28/7,y=35/7`
`⇒ x= 4,y=5`
Hence, the fraction is`4/5`
The sum of the numerator and denominator of a fraction is 4 more than twice the numerator. If the numerator and denominator are increased by 3, they are in the ratio 2 : 3. Determine the fraction.
The present age of a father is three years more than three times the age of the son. Three years hence father's age will be 10 years more than twice the age of the son. Determine their present ages.
Father's age is three times the sum of age of his two children. After 5 years his age will be twice the sum of ages of two children. Find the age of father.
State with reason whether the point (3, −2) will lie on the graph of the equation 5m – 3n = − 21
