Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral finds the angles of the cyclic quadrilateral.
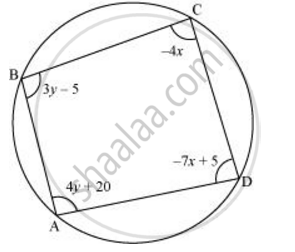
उत्तर
We know that the sum of the measures of opposite angles in a cyclic quadrilateral is 180°.
Therefore, ∠A + ∠C = 180
4y + 20 − 4x = 180
− 4x + 4y = 160
x − y = − 40 (i)
Also, ∠B + ∠D = 180
3y − 5 − 7x + 5 = 180
− 7x + 3y = 180 (ii)
Multiplying equation (i) by 3, we obtain
3x − 3y = − 120 (iii)
Adding equations (ii) and (iii), we obtain
− 7x + 3x = 180 − 120
− 4x = 60
x = −15
By using equation (i), we obtain
x − y = − 40
−15 − y = − 40
y = −15 + 40 = 25
∠A = 4y + 20 = 4(25) + 20 = 120°
∠B = 3y − 5 = 3(25) − 5 = 70°
∠C = − 4x = − 4(− 15) = 60°
∠D = − 7x + 5 = − 7(−15) + 5 = 110°
APPEARS IN
संबंधित प्रश्न
Solve the following pairs of equations by reducing them to a pair of linear equations
`4/x + 3y = 14`
`3/x - 4y = 23`
Formulate the following problems as a pair of equations, and hence find their solutions:
2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
One says, "Give me a hundred, friend! I shall then become twice as rich as you". The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital? [From the Bijaganita of Bhaskara II)
[Hint: x + 100 = 2 (y − 100), y + 10 = 6(x − 10)]
Find the values of following determinant.
`|(7/3,5/3), (3/2, 1/2)|`
The sum of two numbers is 1000 and the difference between their squares is 256000. Find the numbers.
The sum of a two digit number and the number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the number.
The sum of the numerator and denominator of a fraction is 3 less than twice the denominator. If the numerator and denominator are decreased by 1, the numerator becomes half the denominator. Determine the fraction.
Ten years ago, a father was twelve times as old as his son and ten years hence, he will be twice as old as his son will be then. Find their present ages.
Father's age is three times the sum of age of his two children. After 5 years his age will be twice the sum of ages of two children. Find the age of father.
Two years ago, a father was five times as old as his son. Two year later, his age will be 8 more than three times the age of the son. Find the present ages of father and son.
