Advertisements
Advertisements
प्रश्न
Solve the following pair of linear equations.
152x − 378y = − 74
− 378x + 152y = − 604
उत्तर
152x − 378y = − 74
76x − 189y = − 37
`x =(189y - 37)/76 ...(1)`
− 378x + 152y = − 604
− 189x + 76y = − 302 … (2)
Substituting the value of x in equation (2), we obtain
`-189((189y-37)/76)+76y = - 302`
− (189)2 y + 189 × 37 + (76)2 y = − 302 × 76
189 × 37 + 302 × 76 = (189)2 y − (76)2 y
6993 + 22952 = (189 − 76) (189 + 76) y
29945 = (113) (265) y
y = 1
From equation (1), we obtain
`x = (189(1)-37)/76`
`x =(189-37)/76 = 152/76`
x = 2
APPEARS IN
संबंधित प्रश्न
Solve the following simultaneous equations: `7/(2X+1)+13/(Y+2)=27,13/(2X+1)+7/(Y+2)=33`
Solve `\frac{2}{x+2y}+\frac{6}{2x-y}=4\text{ ;}\frac{5}{2( x+2y)}+\frac{1}{3( 2x-y)}=1` where, x + 2y ≠ 0 and 2x – y ≠ 0
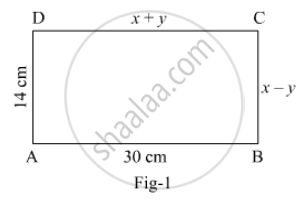
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
Solve the following for x:
`1/(2a+b+2x)=1/(2a)+1/b+1/(2x)`
Find the value of following determinant.
`|(-1,7),(2,4)|`
The sum of two numbers is 8. If their sum is four times their difference, find the numbers.
A two-digit number is such that the product of its digits is 20. If 9 is added to the number, the digits interchange their places. Find the number.
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes 1/2. Find the fraction.
Six years hence a man's age will be three times the age of his son and three years ago he was nine times as old as his son. Find their present ages.
Two years ago, a father was five times as old as his son. Two year later, his age will be 8 more than three times the age of the son. Find the present ages of father and son.
