Advertisements
Advertisements
प्रश्न
Solve the following pair of linear equations.
(a − b) x + (a + b) y = a2− 2ab − b2
(a + b) (x + y) = a2 + b2
उत्तर
(a − b) x + (a + b) y = a2− 2ab − b2 … (1)
(a + b) (x + y) = a2 + b2
(a + b) x + (a + b) y = a2 + b2 … (2)
Subtracting equation (2) from (1), we obtain
(a − b) x − (a + b) x = (a2 − 2ab − b2) − (a2 + b2)
(a − b − a − b) x = − 2ab − 2b2
− 2bx = − 2b (a + b)
x = a + b
Using equation (1), we obtain
(a − b) (a + b) + (a + b) y = a2 − 2ab − b2
a2 − b2 + (a + b) y = a2− 2ab − b2
(a + b) y = − 2ab
`y = (-2ab)/(a+b)`
APPEARS IN
संबंधित प्रश्न
Solve the following pairs of equations by reducing them to a pair of linear equations
`1/(2x) + 1/(3y) = 2`
`1/(3x) + 1/(2y) = 13/6`
Solve the following pairs of equations by reducing them to a pair of linear equations
`1/(3x+y) + 1/(3x-y) = 3/4`
`1/(2(3x-y)) - 1/(2(3x-y)) = (-1)/8`
In a ΔABC, ∠C = 3 ∠B = 2 (∠A + ∠B). Find the three angles.
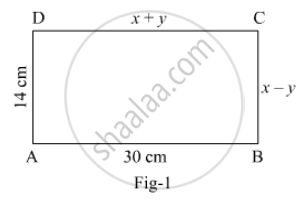
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
A number consist of two digits whose sum is five. When the digits are reversed, the number becomes greater by nine. Find the number.
The sum of digits of a two number is 15. The number obtained by reversing the order of digits of the given number exceeds the given number by 9. Find the given number.
The sum of a two digit number and the number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the number.
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If the numerator is multiplied by 2 and the denominator is reduced by 5, the fraction becomes `6/5`. Thus, we have
`(2x)/(y-5)=6/5`
`⇒ 10x=6(y-5)`
`⇒ 10x=6y-30`
`⇒ 10x-6y+30 =0`
`⇒ 2(5x-3y+15)=0`
`⇒ 5x - 3y+15=0`
If the denominator is doubled and the numerator is increased by 8, the fraction becomes `2/5`. Thus, we have
`(x+8)/(2y)=2/5`
`⇒ 5(x+8)=4y`
`⇒ 5x+40=4y`
`⇒ 5x-4y+40=0`
So, we have two equations
`5x-3y+15=0`
`5x-4y+40=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-3)xx40-(-4)xx15)=-y/(5xx40-5xx15)=1/(5xx(-4)-5xx(-3))`
`⇒ x/(-120+60)=(-y)/(200-75)=1/(-20+15)`
`⇒x/(-60)=-y/125``=1/-5`
`⇒ x= 60/5,y=125/5`
`⇒ x=12,y=25`
Hence, the fraction is `12/25`
The sum of the numerator and denominator of a fraction is 3 less than twice the denominator. If the numerator and denominator are decreased by 1, the numerator becomes half the denominator. Determine the fraction.
Six years hence a man's age will be three times the age of his son and three years ago he was nine times as old as his son. Find their present ages.
