Advertisements
Advertisements
प्रश्न
Solve the following pair of linear equations.
(a − b) x + (a + b) y = a2− 2ab − b2
(a + b) (x + y) = a2 + b2
उत्तर
(a − b) x + (a + b) y = a2− 2ab − b2 … (1)
(a + b) (x + y) = a2 + b2
(a + b) x + (a + b) y = a2 + b2 … (2)
Subtracting equation (2) from (1), we obtain
(a − b) x − (a + b) x = (a2 − 2ab − b2) − (a2 + b2)
(a − b − a − b) x = − 2ab − 2b2
− 2bx = − 2b (a + b)
x = a + b
Using equation (1), we obtain
(a − b) (a + b) + (a + b) y = a2 − 2ab − b2
a2 − b2 + (a + b) y = a2− 2ab − b2
(a + b) y = − 2ab
`y = (-2ab)/(a+b)`
APPEARS IN
संबंधित प्रश्न
Solve `\frac{1}{x+y}+\frac{2}{x-y}=2\text{ and }\frac{2}{x+y}-\frac{1}{x-y}=3` where, x + y ≠ 0 and x – y ≠ 0
Solve the following pairs of equations by reducing them to a pair of linear equations
`1/(2x) + 1/(3y) = 2`
`1/(3x) + 1/(2y) = 13/6`
Solve the following pairs of equations by reducing them to a pair of linear equations
`5/(x-1) + 1/y-2 = 2`
`6/(x-1) - 3/(y-2) = 1`
Solve the following pairs of equations by reducing them to a pair of linear equations
`(7x-2y)/(xy) = 5`
`(8x + 7y)/(xy) = 15`
Solve the following pairs of equations by reducing them to a pair of linear equations
`1/(3x+y) + 1/(3x-y) = 3/4`
`1/(2(3x-y)) - 1/(2(3x-y)) = (-1)/8`
Formulate the following problems as a pair of equations, and hence find their solutions:
2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
Solve the following pair of linear equations: px + qy = p − q, qx − py = p + q
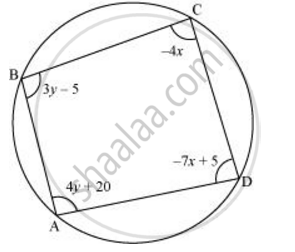
ABCD is a cyclic quadrilateral finds the angles of the cyclic quadrilateral.
Two years ago, a father was five times as old as his son. Two year later, his age will be 8 more than three times the age of the son. Find the present ages of father and son.
