Advertisements
Advertisements
प्रश्न
Ten years ago, a father was twelve times as old as his son and ten years hence, he will be twice as old as his son will be then. Find their present ages.
उत्तर
Let the present age of father be x years and the present age of his son be y years.
After 10 years, father’s age will be (x+10) years and son’s age will be (y + 10) years. Thus using the given information, we have
`x +10 =2(y+10)`
`⇒ x+ 10 = 2y+ 20`
` ⇒ x - 2y -10 =0`
Before 10 years, the age of father was `(x - 10)` years and the age of son was `(y - 10)` years. Thus using the given information, we have
` x-10 =12 (y -10)`
`⇒ x + 10 = 2y +20`
`⇒ x - 12y +110 =0`
So, we have two equations
`x -2y -10 =0`
` x- 12y +110 =0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
` x / ((-2)xx110 -(-12)xx(-10))=(-y)/(1xx110 -1(-10))= 1/(1xx(-12)-1xx(-2))`
`⇒ x / (-220-120)=(-y)/(110+10)+ 1/(-12+2)`
`⇒ x/-340 =(-y)/120 = 1/(-10)`
`⇒ x/(340)= y/120 = 1/10`
`⇒ x = 340/10,y=120/10`
`⇒ x = 34 , y = 12`
Hence, the present age of father is 34 years and the present age of son is 12 years.
APPEARS IN
संबंधित प्रश्न
Solve the following pairs of equations by reducing them to a pair of linear equations
`1/(3x+y) + 1/(3x-y) = 3/4`
`1/(2(3x-y)) - 1/(2(3x-y)) = (-1)/8`
Formulate the following problems as a pair of equations, and hence find their solutions:
Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
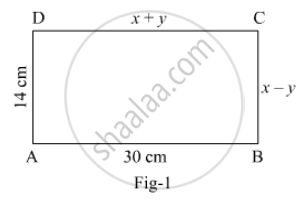
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
Find the value of following determinant.
`|(5,3), (-7,0)|`
A number consist of two digits whose sum is five. When the digits are reversed, the number becomes greater by nine. Find the number.
A two-digit number is 4 times the sum of its digits and twice the product of the digits. Find the number.
The sum of a numerator and denominator of a fraction is 18. If the denominator is increased by 2, the fraction reduces to 1/3. Find the fraction.
The sum of the numerator and denominator of a fraction is 3 less than twice the denominator. If the numerator and denominator are decreased by 1, the numerator becomes half the denominator. Determine the fraction.
