Advertisements
Advertisements
प्रश्न
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
उत्तर
Let the number of rows be x and number of students in a row be y.
Total students of the class
= Number of rows × Number of students in a row
= xy
Using the information given in the question,
Condition 1
Total number of students = (x − 1) (y + 3)
xy = (x − 1) (y + 3) = xy − y + 3x − 3
3x − y − 3 = 0
3x − y = 3 (i)
Condition 2
Total number of students = (x + 2) (y − 3)
xy = xy + 2y − 3x − 6
3x − 2y = −6 (ii)
Subtracting equation (ii) from (i),
(3x − y) − (3x − 2y) = 3 − (−6)
− y + 2y = 3 + 6
y = 9
By using equation (i), we obtain
3x − 9 = 3
3x = 9 + 3 = 12
x = 4
Number of rows = x = 4
Number of students in a row = y = 9
Number of total students in a class = xy = 4 × 9 = 36
APPEARS IN
संबंधित प्रश्न
Solve `\frac{2}{x+2y}+\frac{6}{2x-y}=4\text{ ;}\frac{5}{2( x+2y)}+\frac{1}{3( 2x-y)}=1` where, x + 2y ≠ 0 and 2x – y ≠ 0
Solve the following systems of equations
(i)`\frac{15}{u} + \frac{2}{v} = 17`
`\frac{1}{u} + \frac{1}{v} = \frac{36}{5}`
(ii) ` \frac{11}{v} – \frac{7}{u} = 1`
`\frac{9}{v} + \frac{4}{u} = 6`
Solve the following pairs of equations by reducing them to a pair of linear equations
`4/x + 3y = 14`
`3/x - 4y = 23`
A train covered a certain distance at a uniform speed. If the train would have been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Solve the following pair of linear equations.
152x − 378y = − 74
− 378x + 152y = − 604
ABCD is a cyclic quadrilateral finds the angles of the cyclic quadrilateral.
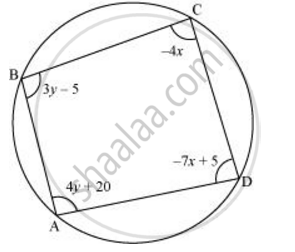
Solve the following for x:
`1/(2a+b+2x)=1/(2a)+1/b+1/(2x)`
Find the value of following determinant.
`|(5,3), (-7,0)|`
On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gains Rs 2000. But if he sells the T.V. at 10% gain the fridge at 5% loss. He gains Rs 1500 on the transaction. Find the actual prices of T.V. and fridge.
A two-digit number is 4 times the sum of its digits and twice the product of the digits. Find the number.
