Advertisements
Advertisements
प्रश्न
A two-digit number is 4 times the sum of its digits and twice the product of the digits. Find the number.
उत्तर
Let the digits at units and tens place of the given number be x and y respectively. Thus, the number is `10 y + x`.
The number is 4 times the sum of the two digits. Thus, we have
` 10 y +x =4( x + y)`
` ⇒ 10y + x = 4x + 4y`
`⇒ 4x + 4y -10y -x =0 `
` ⇒ 3x -6y =0`
`⇒ 3(x - 2y)=0`
` ⇒ x- 2y =0`
` ⇒ x = 2y`
After interchanging the digits, the number becomes `10x + y`.
The number is twice the product of the digits. Thus, we have `10y+x=2xy`
So, we have the systems of equations
` x = 2y,`
` 10y +x =2xy`
Here x and y are unknowns. We have to solve the above systems of equations for xand y.
Substituting `x = 2y` in the second equation, we get
` 10y + 2y = 2xx2yxxy`
` ⇒ 12y = 4y^2`
` ⇒ 4y^2-12y =0`
` ⇒ y ( y -3)=0`
` ⇒ y =0` OR `y = 3`
Substituting the value of y in the first equation, we have
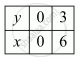
Hence, the number is `10 xx 3+6= 36.`
Note that the first pair of solution does not give a two digit number.
APPEARS IN
संबंधित प्रश्न
Solve `\frac{1}{x+y}+\frac{2}{x-y}=2\text{ and }\frac{2}{x+y}-\frac{1}{x-y}=3` where, x + y ≠ 0 and x – y ≠ 0
Solve the following pairs of equations by reducing them to a pair of linear equations
`1/(3x+y) + 1/(3x-y) = 3/4`
`1/(2(3x-y)) - 1/(2(3x-y)) = (-1)/8`
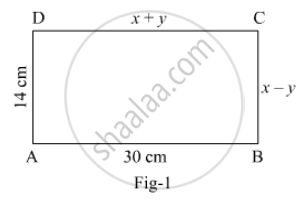
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
Seven times a two-digit number is equal to four times the number obtained by reversing the digits. If the difference between the digits is 3. Find the number.
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If the numerator is multiplied by 2 and the denominator is reduced by 5, the fraction becomes `6/5`. Thus, we have
`(2x)/(y-5)=6/5`
`⇒ 10x=6(y-5)`
`⇒ 10x=6y-30`
`⇒ 10x-6y+30 =0`
`⇒ 2(5x-3y+15)=0`
`⇒ 5x - 3y+15=0`
If the denominator is doubled and the numerator is increased by 8, the fraction becomes `2/5`. Thus, we have
`(x+8)/(2y)=2/5`
`⇒ 5(x+8)=4y`
`⇒ 5x+40=4y`
`⇒ 5x-4y+40=0`
So, we have two equations
`5x-3y+15=0`
`5x-4y+40=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-3)xx40-(-4)xx15)=-y/(5xx40-5xx15)=1/(5xx(-4)-5xx(-3))`
`⇒ x/(-120+60)=(-y)/(200-75)=1/(-20+15)`
`⇒x/(-60)=-y/125``=1/-5`
`⇒ x= 60/5,y=125/5`
`⇒ x=12,y=25`
Hence, the fraction is `12/25`
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If 3 is added to the denominator and 2 is subtracted from the numerator, the fraction becomes `1/4`. Thus, we have
`(x-2)/(y+3)=1/4`
`⇒ 4(x-2)=y+3`
`⇒ 4x-8=y+3`
`⇒ 4x-y-11=0`
If 6 is added to the numerator and the denominator is multiplied by 3, the fraction becomes `2/3`. Thus, we have
`(x+6)/(3y)=2/3`
`⇒ 3(x+6)=6y`
`⇒ 3x +18 =6y`
`⇒ 3x-6y+18=0`
`⇒ 3(x-2y+6)=0`
`⇒ x-3y+6=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-1)xx6-(-2)xx(-11))=(-y)/(4xx6-1xx(-11))=1/(4xx(-2)-1xx(-1))`
`⇒ x/(-6-22)=-y/(24+11)=1/(-8+1)`
`⇒ x/-28=-y/35=1/-7`
`⇒ x= 28/7,y=35/7`
`⇒ x= 4,y=5`
Hence, the fraction is`4/5`
If 2 is added to the numerator of a fraction, it reduces to 1/2 and if 1 is subtracted from the denominator, it reduces to 1/3. Find the fraction.
Ten years later, A will be twice as old as B and five years ago, A was three times as old as B. What are the present ages of A and B?
Father's age is three times the sum of age of his two children. After 5 years his age will be twice the sum of ages of two children. Find the age of father.
Two years ago, a father was five times as old as his son. Two year later, his age will be 8 more than three times the age of the son. Find the present ages of father and son.
