Advertisements
Advertisements
Question
A two-digit number is 4 times the sum of its digits and twice the product of the digits. Find the number.
Solution
Let the digits at units and tens place of the given number be x and y respectively. Thus, the number is `10 y + x`.
The number is 4 times the sum of the two digits. Thus, we have
` 10 y +x =4( x + y)`
` ⇒ 10y + x = 4x + 4y`
`⇒ 4x + 4y -10y -x =0 `
` ⇒ 3x -6y =0`
`⇒ 3(x - 2y)=0`
` ⇒ x- 2y =0`
` ⇒ x = 2y`
After interchanging the digits, the number becomes `10x + y`.
The number is twice the product of the digits. Thus, we have `10y+x=2xy`
So, we have the systems of equations
` x = 2y,`
` 10y +x =2xy`
Here x and y are unknowns. We have to solve the above systems of equations for xand y.
Substituting `x = 2y` in the second equation, we get
` 10y + 2y = 2xx2yxxy`
` ⇒ 12y = 4y^2`
` ⇒ 4y^2-12y =0`
` ⇒ y ( y -3)=0`
` ⇒ y =0` OR `y = 3`
Substituting the value of y in the first equation, we have
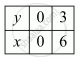
Hence, the number is `10 xx 3+6= 36.`
Note that the first pair of solution does not give a two digit number.
APPEARS IN
RELATED QUESTIONS
Solve the following systems of equations
(i)`\frac{15}{u} + \frac{2}{v} = 17`
`\frac{1}{u} + \frac{1}{v} = \frac{36}{5}`
(ii) ` \frac{11}{v} – \frac{7}{u} = 1`
`\frac{9}{v} + \frac{4}{u} = 6`
Solve the following pairs of equations by reducing them to a pair of linear equations
`10/(x+y) + 2/(x-y) = 4`
`15/(x+y) - 5/(x-y) = -2`
Formulate the following problems as a pair of equations, and hence find their solutions:
Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current
Solve the following for x:
`1/(2a+b+2x)=1/(2a)+1/b+1/(2x)`
A two-digit number is 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number.
A two-digit number is 4 more than 6 times the sum of its digits. If 18 is subtracted from the number, the digits are reversed. Find the number.
If 2 is added to the numerator of a fraction, it reduces to 1/2 and if 1 is subtracted from the denominator, it reduces to 1/3. Find the fraction.
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes 1/2. Find the fraction.
A father is three times as old as his son. After twelve years, his age will be twice as that of his son then. Find the their present ages.
Father's age is three times the sum of age of his two children. After 5 years his age will be twice the sum of ages of two children. Find the age of father.
