Advertisements
Advertisements
Question
If 2 is added to the numerator of a fraction, it reduces to 1/2 and if 1 is subtracted from the denominator, it reduces to 1/3. Find the fraction.
Solution
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If 2 is added to the numerator of the fraction, it reduces to `1/2`. Thus, we have
`(x+2)/y=1/2`
`⇒ 2(x+2)=y`
`⇒ 2x+4 =y`
`⇒ 2x -y+4=0`
If 1 is subtracted from the denominator, the fraction reduces to `1/3`. Thus, we have
`x/(y-1)=1/3`
`⇒ 3x = y-1`
`⇒ 3x -y +1=0`
So, we have two equations
`2x - y+4=0`
`3x -y +1=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((1-)xx1-1(-1)xx4)=(-y)/(2xx1-3xx4)=1/(2xx(-1)-3xx(-1))`
`⇒ x/(-1+4)=(-y)/(2-12)=1/(-2+13)`
`⇒ x/3=-y/-10=1/1`
`⇒ x/3=y/10=1`
`⇒ x/3= y/10=1`
`⇒ x=3,y=10`
Hence, the fraction is`3/10`
APPEARS IN
RELATED QUESTIONS
Solve the following simultaneous equations: `7/(2X+1)+13/(Y+2)=27,13/(2X+1)+7/(Y+2)=33`
The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju
Solve the following pair of linear equations
ax + by = c
bx + ay = 1 + c
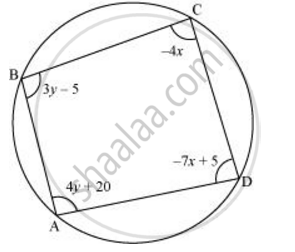
ABCD is a cyclic quadrilateral finds the angles of the cyclic quadrilateral.
A and B each have a certain number of mangoes. A says to B, "if you give 30 of your mangoes, I will have twice as many as left with you." B replies, "if you give me 10, I will have thrice as many as left with you." How many mangoes does each have?
A number consist of two digits whose sum is five. When the digits are reversed, the number becomes greater by nine. Find the number.
The sum of a two digit number and the number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the number.
A two-digit number is 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number.
Ten years later, A will be twice as old as B and five years ago, A was three times as old as B. What are the present ages of A and B?
Two equations in two variables taken together are called ______.
