Advertisements
Advertisements
Question
A number consist of two digits whose sum is five. When the digits are reversed, the number becomes greater by nine. Find the number.
Solution
Let the digits at units and tens place of the given number be x and y respectively. Thus, the number is `10 y + x`.
The sum of the digits of the number is 5. Thus, we have `x + y = 5`
After interchanging the digits, the number becomes `10 x + y`.
The number obtained by interchanging the digits is greater by 9 from the original number. Thus, we have
`10 x + y = 10 y + x + 9`
`⇒ 10 x + y - 10y - x =9`
` ⇒ 9x -9 y = 9 `
`⇒ 9 ( x - y)= 9`
` ⇒ x - y = 9/9`
` ⇒ x - y = 1`
Here x and y are unknowns. We have to solve the above equations for x and y.
Adding the two equations, we have
`( x + y) + ( x - y) = 5 + 1`
`⇒ x + y + x - y = 6`
` ⇒ 2x = 6`
` ⇒ x = 6/2`
` ⇒ x = 3`
Substituting the value of x in the first equation, we have
` 3 + y = 5`
`⇒ y = 5-3`
` ⇒ y = 2`
Hence, the number is ` 10 xx2 + 3 = 23 `
APPEARS IN
RELATED QUESTIONS
Solve the following systems of equations
(i)`\frac{15}{u} + \frac{2}{v} = 17`
`\frac{1}{u} + \frac{1}{v} = \frac{36}{5}`
(ii) ` \frac{11}{v} – \frac{7}{u} = 1`
`\frac{9}{v} + \frac{4}{u} = 6`
Solve the following pairs of equations by reducing them to a pair of linear equations
`(7x-2y)/(xy) = 5`
`(8x + 7y)/(xy) = 15`
In a ΔABC, ∠C = 3 ∠B = 2 (∠A + ∠B). Find the three angles.
Solve the following pair of linear equations
ax + by = c
bx + ay = 1 + c
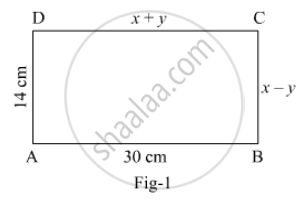
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
The sum of digits of a two number is 15. The number obtained by reversing the order of digits of the given number exceeds the given number by 9. Find the given number.
A two-digit number is 3 more than 4 times the sum of its digits. If 8 is added to the number, the digits are reversed. Find the number.
A two-digit number is 4 more than 6 times the sum of its digits. If 18 is subtracted from the number, the digits are reversed. Find the number.
The numerator of a fraction is 4 less than the denominator. If the numerator is decreased by 2 and denominator is increased by 1, then the denominator is eight times the numerator. Find the fraction.
State with reason whether the point (3, −2) will lie on the graph of the equation 5m – 3n = − 21
