Advertisements
Advertisements
Question
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
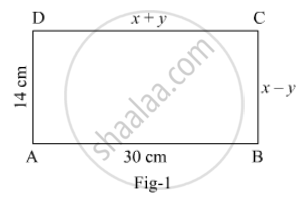
Solution
In rectangle ABCD, DC = AB and BC = AD
⇒ x + y = 30 .....(i) and x − y = 14 .....(ii)
Adding (i) and (ii), we get
2x = 44
⇒ x = 22
Put x = 22 in (i), we get y = 8
Hence, x = 22 and y = 8.
APPEARS IN
RELATED QUESTIONS
Solve the following system of equations `\frac { 1 }{ 2x } – \frac { 1 }{ y } = – 1; \frac { 1 }{ x } + \frac { 1}{ 2y } = 8`
Solve `\frac{2}{x+2y}+\frac{6}{2x-y}=4\text{ ;}\frac{5}{2( x+2y)}+\frac{1}{3( 2x-y)}=1` where, x + 2y ≠ 0 and 2x – y ≠ 0
Solve the following pairs of equations by reducing them to a pair of linear equations
`10/(x+y) + 2/(x-y) = 4`
`15/(x+y) - 5/(x-y) = -2`
Solve the following pair of linear equations.
`x/a-y/b = 0`
ax + by = a2 + b2
A number consist of two digits whose sum is five. When the digits are reversed, the number becomes greater by nine. Find the number.
The sum of a two digit number and the number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the number.
The numerator of a fraction is 4 less than the denominator. If the numerator is decreased by 2 and denominator is increased by 1, then the denominator is eight times the numerator. Find the fraction.
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If the numerator is multiplied by 2 and the denominator is reduced by 5, the fraction becomes `6/5`. Thus, we have
`(2x)/(y-5)=6/5`
`⇒ 10x=6(y-5)`
`⇒ 10x=6y-30`
`⇒ 10x-6y+30 =0`
`⇒ 2(5x-3y+15)=0`
`⇒ 5x - 3y+15=0`
If the denominator is doubled and the numerator is increased by 8, the fraction becomes `2/5`. Thus, we have
`(x+8)/(2y)=2/5`
`⇒ 5(x+8)=4y`
`⇒ 5x+40=4y`
`⇒ 5x-4y+40=0`
So, we have two equations
`5x-3y+15=0`
`5x-4y+40=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-3)xx40-(-4)xx15)=-y/(5xx40-5xx15)=1/(5xx(-4)-5xx(-3))`
`⇒ x/(-120+60)=(-y)/(200-75)=1/(-20+15)`
`⇒x/(-60)=-y/125``=1/-5`
`⇒ x= 60/5,y=125/5`
`⇒ x=12,y=25`
Hence, the fraction is `12/25`
The sum of the numerator and denominator of a fraction is 3 less than twice the denominator. If the numerator and denominator are decreased by 1, the numerator becomes half the denominator. Determine the fraction.
Asha has only ₹1 and ₹2 coins with her. If the total number of coins that she has is 50 and the amount of money with her is ₹75, then the number of ₹1 and ₹2 coins are, respectively.
