Advertisements
Advertisements
प्रश्न
Solve graphically : 2x – 5y ≥10
उत्तर
Consider the line whose equation is 2x – 5y = 10. To find the points of intersection of this line with the coordinate axes.
Put y = 0, we get x = 10, i.e. x = 5,
∴ A = (5, 0) is a point on the line.
Put x = 0, we get –5y = 10, i.e. y = –2
∴ B = (0, –2) is another point on the line.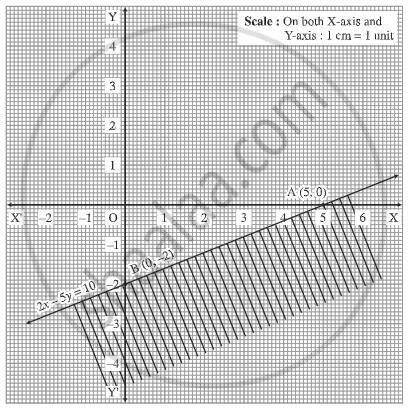
Draw the line AB joining these points. This line divide the plane in two parts.
1. Origin side
2. Non-origin side
To find the solution set, we have to check the position of the origin (0,0) with respect to the line.
when x = 0, y = 0, then 2x – 5y = 0 which is neither greater non equal to 10.
∴ 2x – 5y `cancel>=`10 in the case.
Hence (0,0) will not lie in the required region.
Therefore, the given inequality is the non-origin side, which is shaded in the graph.
This is the solution set of 2x – 5y ≥10.
APPEARS IN
संबंधित प्रश्न
Solve graphically: x ≥ 0
Solve graphically : y ≥ 0
Solve graphically : x ≤ 0
Solve graphically : y ≤ 0
Solve graphically : x ≥ 0 and y ≥ 0
Solve graphically: x ≤ 0 and y ≥ 0
Solve graphically : x ≤ 0 and y ≤ 0
Solve graphically: 2x – 3 ≥ 0
Solve graphically : 5y + 3 ≤ 0
Solve graphically : x +2y ≤ 6
Solve graphically : 5x – 3y ≤ 0
Solve graphically : x – y ≤ 2 and x + 2y ≤ 8
Solve graphically : x + y ≥ 6 and x + 2y ≤ 10
The value of objective function is maximum under linear constraints
If a corner point of the feasible solutions are (0, 10) (2, 2) (4, 0) (3, 2) then the point of minimum Z = 3x + 2y is
For the constraint of a linear optimizing function z = 3x1 + 11x2, given by 2x1 + x2 ≤ 2, 4x1 + x2 ≥ 4 and x1, x2 ≥ 0
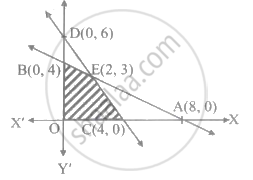
The shaded region is represented by the in equations ______
Region represented by the inequalities x ≥ 0, y ≤ 0 is ______.
Solution set of the inequality y ≥ 0 is ______.
Which of the following linear inequalities satisfy the shaded region of the given figure?
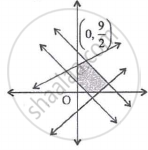
The object function z = 4x1 + 5x2, subject to 2x1 + x2 ≥ 7, 2x1 + 3x2 ≤ 15, x2 ≤ 3, x1, x2 ≥ 0 has minimum value at the point is ______.
The objective function of LPP defined over the convex set attains it optimum value at ______.
