Advertisements
Advertisements
प्रश्न
Solve the following inequation and graph the solution set,
2x - 5 ≤ 5x + 4 < 11n ∈ R.
उत्तर
Here, 2x - 5 ≤ 5x + 4 < 11
⇒ 2x - 5 ≤ 5x + 4 and 5x + 4 < 11
⇒ -3x < 9 and 5x < 7
⇒ x ≥ - 3 and x < `(7)/(5)`
∴ Solution set = `{x : -3 ≤ x ≤ (7)/(5) and x ∈ "R"}`.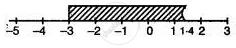
APPEARS IN
संबंधित प्रश्न
State, whether the following statements are true or false:
a < b, then a – c < b – c
If 25 – 4x ≤ 16, find:
- the smallest value of x, when x is a real number.
- the smallest value of x, when x is an integer.
Represent the solution of the following inequalities on the real number line:
2 – 3x > 7 – 5x
x ∈ {real numbers} and –1 < 3 – 2x ≤ 7, evaluate x and represent it on a number line.
If 5x – 3 ≤ 5 + 3x ≤ 4x + 2, express it as a ≤ x ≤ b and then state the values of a and b.
Solve for x : 7 + 5x > x - 13, where x is a negative integer.
For each inequality, determine which of the given numbers are in the solution set:
16 - 5 x ≤ - 4; 4, -3, 10.
Solve the following inequalities in the given universal set:
2x - 5 ≤ 5x + 4 < 11, where x ∈ I.
Solve the following inequalities and graph their solution set:
`(x + 8)/(x + 1) > 1`.
The maximum value of x for the inequation 4x ≤ 12 + x is ______.
