Question

State Newton’s three laws and discuss their significance.

Answer 1

First Law:

Every object continues to be in the state of rest or of uniform motion (constant velocity) unless there is an external force acting on it.

Second Law:

The force acting on an object is equal to the rate of change of its momentum

Third Law:

For every action, there is an equal and opposite reaction.

Significance of Newton’s Laws:

1. Newton’s laws are vector laws. The equation `overlineF = moverlinea` is a vector equation and essentially it is equal to three scalar equations. In Cartesian coordinates, this equation can be written as `F_xhati + F_yhatj + F_zhatj = ma_xhati + ma_yhatj + ma_zhatj`

By comparing both sides, the three scalar equations are

F_x = ma_x The acceleration along the x-direction depends only on the component of force acting along the x-direction.
F_y = ma_y The acceleration along the y-direction depends only on the component of force acting along the y-direction.
F_z = ma_z The acceleration along the z-direction depends only on the component of force acting along the z-direction.
From the above equations, we can infer that the force acting along the y-direction cannot alter the acceleration along the x-direction. In the same way, F_z cannot affect a_y and a_x. This understanding is essential for solving problems.

2. The acceleration experienced by the body at time t depends on the force which acts on the body at that instant of time. It does not depend on the force which acted on the body before the time t. This can be expressed as `overlineF(t) = moverlinea(t)`

Acceleration of the object does not depend on the previous history of the force. For example, when a spin bowler or a fast bowler throws the ball to the batsman, once the ball leaves the hand of the bowler, it experiences only gravitational force and air frictional force. The acceleration of the ball is independent of how the ball was bowled (with a lower or a higher speed).

3. In general, the direction of a force may be different from the direction of motion. Though in some cases, the object may move in the same direction as the direction of the force, it is not always true. A few examples are given below.

Case 1:

Force and motion in the same direction:
When an apple falls towards the Earth, the direction of motion (direction of velocity) of the apple and that of force are in the same downward direction as shown in the Figure.

(a) Force and motion in the same direction

Case 2:

Force and motion not in the same direction:
The Moon experiences a force towards the Earth. But it actually moves in an elliptical orbit. In this case, the direction of the force is different from the direction of motion as shown in Figure.

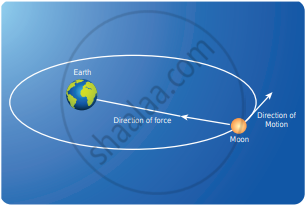
(b) A moon orbiting an elliptical orbit around the earth

Case 3:

Force and motion in opposite direction:
If an object is thrown vertically upward, the direction of motion is upward, but the gravitational force is downward as shown in the Figure.

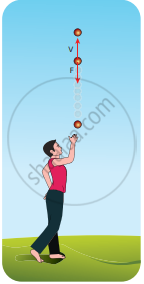
(c) Force and direction of motion are in opposite directions

Case 4:

Zero net force, but there is motion:
When a raindrop gets detached from the cloud it experiences both downward gravitational force and upward air drag force. As it descends towards the Earth, the upward air drag force increases, and after a certain time, the upward air drag force cancels the downward gravity. From then on the raindrop moves at constant velocity till it touches the surface of the Earth. Hence the raindrop comes with zero net force, therefore with zero acceleration but with non-zero terminal velocity. It is shown in the Figure.

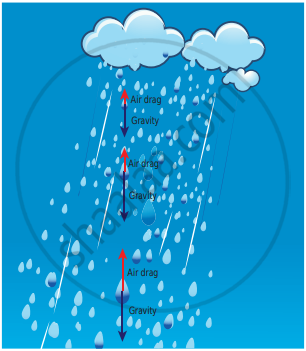
(d) Zero net force and non zero terminal velocity

4. If multiple forces `vecF_1, vecF_2, vecF_3,......vecF_n` act on the same body, then the total force (`vecF_"net"`) is equivalent to the vectorial sum of the individual forces. Their net force provides the acceleration.
`vecF_"net" = vecF_1 + vecF_2 + vecF_3 + ...... + vecF_n`

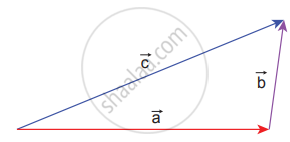
Vector addition of forces

Newton’s second law for this case is – 

`vecF_"net" = moverlinea`

In this case, the direction of acceleration is in the direction of the net force.

Example:

Bow and arrow

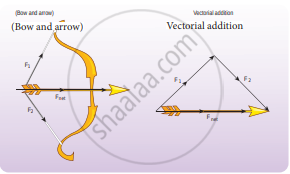
Bow and arrow – Net force is on the arrow

5. Newton’s second law can also be written in the following form. Since the acceleration is the second derivative of the position vector of the body `(veca = (d^2vecr)/(dt^2))` the force on the body is - `overlineF = m(d^2vecr)/(dt^2)`

From this expression, we can infer that Newton’s second law is basically a second-order ordinary differential equation and whenever the second derivative of the position vector is not zero, there must be a force acting on the body.

6. If no force acts on the body then Newton’s second law, m = `(dvecv)/dt` = 0
It implies that `overlinev` = constant. It is essentially Newton’s first law. It implies that the second law is consistent with the first law. However, it should not be thought of as the reduction of the second law to the first when no force acts on the object. Newton’s first and second laws are independent laws. They can internally be consistent with each other but cannot be derived from each other.

7. Newton’s second law is cause and effect relation. Force is the cause and acceleration is the effect. Conventionally, the effect should be written on the left and cause on the right-hand side of the equation. So the correct way of writing Newton’s second law is –
`moverlinea = overlineF` or `(dvecp)/dt = overlineF`