Advertisements
Advertisements
प्रश्न
Briefly explain the origin of friction. Show that in an inclined plane, the angle of friction is equal to the angle of repose.
उत्तर
If a very gentle force in the horizontal direction is given to an object at rest on the table it does not move. It is because of the opposing force exerted by the surface on the object which resists its motion. This force is called the frictional force. During the time of Newton and Galileo, a frictional force was considered as one of the natural forces like a gravitational force. But in the twentieth century, the understanding of atoms, electrons, and protons has changed the perspective.
The frictional force is actually the electromagnetic force between the atoms on the two surfaces. Even well-polished surfaces have irregularities on the surface at the microscopic level. The component of force parallel to the inclined plane (mg sin θ) tries to move the object down. The component of force perpendicular to the inclined plane (mg cos θ) is balanced by the Normal force (N).
N = mg cos θ ………(1)
When the object just begins to move, the static friction attains its maximum value
`f_s = f_s^"max" = mu_sN`
This friction also satisfies the relation
`f_s^"max"` = µs mg sin θ ……….(2)
Equating the right-hand side of equations (1) and (2),
`(f_s^"max")"/"N = sintheta/costheta`
From the definition of angle of friction, we also know that
tan θ = µs ………..(3)
in which θ is the angle of friction.
Thus the angle of repose is the same as the angle of friction. But the difference is that the angle of repose refers to inclined surfaces and the angle of friction is applicable to any type of surface.
APPEARS IN
संबंधित प्रश्न
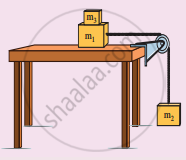
Two masses m1 and m2 are connected with a string passing over a frictionless pulley fixed at the comer of the table as shown in the figure. The coefficient of static friction of mass m1 with the table is µs Calculate the minimum mass m3 that may be placed on m1 to prevent it from sliding. Check if m1 = 15 kg, m2 = 10 kg, m3 = 25 and µs = 0.2.
A heavy uniform chain lies on a horizontal table. If the coefficient of friction between the chain and the table is 0.25, then the maximum fraction of the length of the chain that can hang over one edge of the table is
A uniform metal chain is placed on a rough table such that one end of the chain hangs down over the edge of the table. When two-thirds of its chain length hangs over the edge the chain start sliding. Then the coefficient of static friction is:
A uniform chain of length 3 metres and mass 3 kg overhangs a smooth table with 2 metres laying on the table. If k is the kinetic energy of the chain in joule as it completely slips off the table, then the value of k is ______.
(Take g = 10 m/s2)
A 40 kg wooden crate is being pushed across a wooden floor with a force of 160 N. If µk = 0.3, the acceleration of the crate is ______ m/s2. (g = 10 m/s2}
A block of mass m = 1 kg moving on horizontal surface with speed u = 2 m/s enters a rough horizontal patch ranging from x = 0.10 m to x = 2.00 m. If the retarding force fr on the block in this range is inversely proportional to x over this range i.e.
fr = `"-k"/x` 0.10 < x < 2.00
= 0 for x < 0.10 and x > 2.00
If k = 0.5 J then the speed of this block as it crosses the patch is (use ℓn 20 = 3)
The minimum radius of a circle along which a cyclist can ride with a velocity 18 km/hr if the coefficient of friction between the tyres and the road is µ = 0.5, is ______ (Take g = 10 m/s2)
Starting from rest, a body slides down a 45° inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is ______.
A block of mass 10 kg starts sliding on a surface with an initial velocity of 9.8 ms-1. The coefficient of friction between the surface and bock is 0.5. The distance covered by the block before coming to rest is ______.
[use g = 9.8 ms-2]
A body starts from rest on a long inclined plane of slope 45°. The coefficient of friction between the body and the plane varies as µ = 0.3 x, where x is distance travelled down the plane. The body will have maximum speed (for g = 10 m/s2) when x = ______.
