Advertisements
Advertisements
प्रश्न
Surface tension is exhibited by liquids due to force of attraction between molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat of vaporisation for water Lv = 540 k cal kg–1, the mechanical equivalent of heat J = 4.2 J cal–1, density of water ρw = 103 kg l–1, Avagadro’s No NA = 6.0 × 1026 k mole–1 and the molecular weight of water MA = 18 kg for 1 k mole.
- Estimate the energy required for one molecule of water to evaporate.
- Show that the inter–molecular distance for water is `d = [M_A/N_A xx 1/ρ_w]^(1/3)` and find its value.
- 1 g of water in the vapor state at 1 atm occupies 1601 cm3. Estimate the intermolecular distance at boiling point, in the vapour state.
- During vaporisation a molecule overcomes a force F, assumed constant, to go from an inter-molecular distance d to d ′. Estimate the value of F.
- Calculate F/d, which is a measure of the surface tension.
उत्तर
a. According to the problem, latent heat of vaporisation for water
`(L_v) = 540 k cal = 540 xx 10^3 xx 4.2 J = 2268 xx 10^3 J`
Therefore, energy required to evaporate 1 kmol (18 kg) of water
= `(2268 xx 10^3 J)(18)`
= `40824 xx 10^3 J`
= `4.0824 xx 10^7 J`
Since, there are NA molecules in MA kg of water, the energy required for 1 molecule to evaporate is
`U = (M_AL_v)/N_A J` .....[Where NA = 6 × 1026 = Avogadro number]
`U = (4.0824 xx 10^7)/(6 xx 10^26) J`
= `0.68 xx 10^-19 J`
= `6.8 xx 10^-20 J`
b. Let the water molecules to be at points and are placed at a distance d from each other,
The volume of Na molecule of water = `M_A/ρ_w`
Thus, the volume around one molecule is = `"Volume of 1 kmol"/"Number of molecules/kmol"`
= `M_A/(N_Aρ_w)`
And also volume around one molecule = d3
Thus, by equating these, we get
`d^3 = M_A/(N_Aρ_w)`
∴ `d = (M_A/(N_Aρ_w))^(1/3)`
= `(18/(6 xx 10^26 xx 10^3))^(1/3)`
= `(30 xx 10^-30)^(1/3) m`
= `3.1 xx 10^-10 m`
c. The volume occupied by 18 kg water vapour = `18 xx 1601 xx 10^-6 cm^3`
Number of molecules in 18 kg water = `6 xx 10^26`
Since `6 xx 10^26` molecules occupies `18 xx 1601 xx 10^-3 m^3`
∴ Volume occupied by 1 molecule = `(28818 xx 10^-3 m^3)/(6 xx 10^26)`
= `48030 xx 10^-30 m^3`
If d' is the intermolecular distance, then
`(d)^3 = 48030 xx 10^-30 m^3`
So, `d^' = 36.3 xx 10^-10 m = 36.3 xx 10^-10 m`
d. Work done to change the distance from d to d' is `U = F(d^' - d)`,
This work done is equal to energy required to evaporate 1 molecule.
∴ `F(d^' - d) = 6.8 xx 10^-20`
or `F = (6.8 xx 10^-20)/(d^' - d)`
= `(6.8 xx 10^-20)/((36.3 xx 10^-10 - 3.1 xx 10^-10))`
= `2.05 xx 10^-11 N`
e. Surface tension = `F/d`
= `(2.05 xx 10^-11)/(3.1 xx 10^-10)`
= `6.6 xx 10^-2` N/m
APPEARS IN
संबंधित प्रश्न
Draw a neat labelled diagram showing forces acting on the meniscus of water in a capillary tube.
In a conical pendulum, a string of length 120 cm is fixed at rigid support and carries a mass
of 150 g at its free end. If the mass is revolved in a horizontal circle of radius 0.2 m around a
vertical axis, calculate tension in the string (g = 9.8 m/s2)
If more air is pushed in a soap bubble, the pressure in it
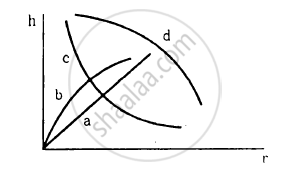
Which of the following graphs may represent the relation between the capillary rise hand the radius r of the capillary?
The lower end of a capillary tube is immersed in mercury. The level of mercury in the tube is found to be 2 cm below the outer level. If the same tube is immersed in water, up to what height will the water rise in the capillary?
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyn/cm.
The surface tension of a liquid at critical temperature is ______
Define the surface tension of a liquid.
What are the factors affecting the surface tension of a liquid?
When one end of the capillary is dipped in water, the height of water column is 'h'. The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of water column. The inner circumference of capillary is ______.
(Surface tension of water = 7 × 10-2 N/m)
