Advertisements
Advertisements
प्रश्न
The adjoining figure shows two straight lines AB and CD intersecting at point P. If ∠BPC = 4x – 5° and ∠APD = 3x + 15°; find:

(i) the value of x.
(ii) ∠APD
(iii) ∠BPD
(iv) ∠BPC
उत्तर
(i) 4x - 5 = 3x + 15 (∵ ∠CPB = ∠APD; opposite angles)
⇒ 4x - 3x = 15 + 5
⇒ x = 20
(ii) ∠APD = 3x + 15
= (3 × 20) + 15
= 60 + 15 = 75°
(iii) ∠BPD = 180 - ∠BPC
= 180 - (4x - 5)
= 180 - 4x + 5
= 185 - (4 × 20)
= 185 - 80 = 105°
(iv) ∠BPC = 4x - 5
= (4 × 20) - 5
= 80 - 5
= 75°
APPEARS IN
संबंधित प्रश्न
In your note-book copy the following angle using ruler and a pair compass only.
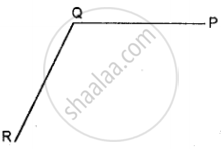
Construct the 60° angle, using ruler and a pair of compass only.
Construct the 30° angle, using ruler and a pair of compass only.
Construct the 135° angle, using ruler and a pair of compass only.
Draw ∠ABC = 120°. Bisect the angle using ruler and compasses. Measure each angle so obtained and check whether or not the new angles obtained on bisecting ∠ABC are equal.
In the following figure, AB is parallel to CD; find the values of angles x, y and z:
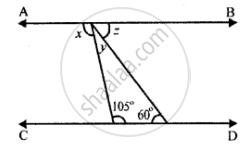
In the following figure, AB is parallel to CD; find the values of angles x, y and z:

In the following figures, PQ is parallel to RS. Find the angles a, b and c:

Two straight lines are cut by a transversal. Are the corresponding angles always
Without using set squares, construct angle ABC = 60° in which AB = BC = 5 cm. Join A and C and measure the length of AC.
