Advertisements
Advertisements
प्रश्न
The angles of quadrilateral are in the ratio 3: 5: 9: 13. Find all the angles of the quadrilateral.
उत्तर
Let the common ratio between the angles be x. Therefore, the angles will be 3x, 5x, 9x, and 13xrespectively.
As the sum of all interior angles of a quadrilateral is 360º,
∴ 3x + 5x + 9x + 13x = 360º
30x = 360º
x = 12º
Hence, the angles are
3x = 3 × 12 = 36º
5x = 5 × 12 = 60º
9x = 9 × 12 = 108º
13x = 13 × 12 = 156º
APPEARS IN
संबंधित प्रश्न
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
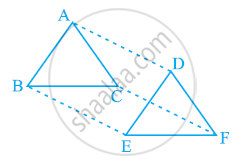
In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see the given figure). Show that
(i) Quadrilateral ABED is a parallelogram
(ii) Quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) Quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ΔABC ≅ ΔDEF.
In a parallelogram ABCD, ∠D = 135°, determine the measures of ∠A and ∠B
The following statement are true and false.
In a parallelogram, the diagonals bisect each other.
If ABCD is a rhombus with ∠ABC = 56°, find the measure of ∠ACD.
The perimeter of a parallelogram is 22 cm. If the longer side measures 6.5 cm, what is the measure of shorter side?
Complete the following statement by means of one of those given in brackets against each:
If one angle of a parallelogram is a right angle, then it is necessarily a .................
The bisectors of any two adjacent angles of a parallelogram intersect at
ABCD is a parallelogram, M is the mid-point of BD and BM bisects ∠B. Then ∠AMB =
Diagonals of a quadrilateral ABCD bisect each other. If ∠A= 45°, then ∠B =
