Question

The area (in sq.units) of the part of the circle x² + y² = 36, which is outside the parabola y² = 9x, is ______.

विकल्प

• `24π + 3sqrt(3)`

• `12π + 3sqrt(3)`

• `12π - 3sqrt(3)`

• `24π - 3sqrt(3)`

Answer 1

The area (in sq.units) of the part of the circle x² + y² = 36, which is outside the parabola y² = 9x, is `underlinebb(24π - 3sqrt(3))`.

Explanation:

Given: Circle 2 + y² = 36

Parabola y² = 9x

Solve equations to find point of intersection.

x² + 9x – 36 = 0

⇒ x = –12, 3

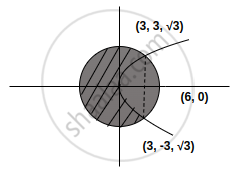
Required area = `πr^2 - 2[int_0^3 sqrt(9x)dx + int_3^6sqrt(36 - x^2)dx]`

= `36π - 12sqrt(3) - 2(x/2sqrt(36 - x^2) + 18sin^-1(x/6))_3^6`

= `36π - 12sqrt(3) - 2(9π - ((9sqrt(3))/2 + 3π))`

= `24π - 3sqrt(3)` sq.units