Topics
Unit 1
Introduction to Micro and Macro Economics
Mathematical Logic
Mathematical Logic
Matrices
- Determinant of a Matrix
- Types of Matrices
- Algebra of Matrices
- Properties of Matrices
- Elementary Transformations
- Inverse of Matrix
- Application of Matrices
- Properties of Transpose of a Matrix
Differentiation
- Derivatives of Composite Functions - Chain Rule
- Derivatives of Inverse Functions
- Derivatives of Logarithmic Functions
- Derivatives of Implicit Functions
- Derivatives of Parametric Functions
- Second Order Derivative
Applications of Derivatives
- Introduction of Derivatives
- Increasing and Decreasing Functions
- Maxima and Minima
- Application of Derivatives to Economics
Integration
Definite Integration
- Fundamental Theorem of Integral Calculus
- Properties of Definite Integrals
Applications of Definite Integration
- Standard Forms of Parabola and Their Shapes
- Standard Forms of Ellipse
- Area Under Simple Curves
Differential Equation and Applications
- Differential Equations
- Order and Degree of a Differential Equation
- Formation of Differential Equation by Eliminating Arbitary Constant
- Differential Equations with Variables Separable Method
- Homogeneous Differential Equations
- Linear Differential Equations
- Application of Differential Equations
Matrices
Commission, Brokerage and Discount
- Commission and Brokerage Agent
- Discount
Insurance and Annuity
- Concept of Insurance
- Fire Insurance
- Accident Insurance
- Marine Insurance
- Annuity
Linear Regression
- Regression
- Types of Linear Regression
- Fitting Simple Linear Regression
- The Method of Least Squares
- Lines of Regression of X on Y and Y on X Or Equation of Line of Regression
- Properties of Regression Coefficients
Time Series
- Introduction to Time Series
- Uses of Time Series Analysis
- Components of a Time Series
- Mathematical Models
- Measurement of Secular Trend
Index Numbers
- Index Numbers
- Types of Index Numbers
- Index Numbers - Terminology and Notation
- Construction of Index Numbers
- Simple Aggregate Method
- Weighted Aggregate Method
- Cost of Living Index Number
- Method of Constructing Cost of Living Index Numbers - Aggregative Expenditure Method
- Method of Constructing Cost of Living Index Numbers - Family Budget Method
- Uses of Cost of Living Index Number
Linear Programming
- Introduction of Linear Programming
- Linear Programming Problem (L.P.P.)
- Mathematical Formulation of Linear Programming Problem
Assignment Problem and Sequencing
- Assignment Problem
- Hungarian Method of Solving Assignment Problem
- Special Cases of Assignment Problem
- Sequencing Problem
- Types of Sequencing Problem
- Finding an Optimal Sequence
Probability Distributions
- Mean of a Random Variable
- Types of Random Variables
- Random Variables and Its Probability Distributions
- Probability Distribution of Discrete Random Variables
- Probability Distribution of a Continuous Random Variable
- Binomial Distribution
- Bernoulli Trial
- Mean of Binomial Distribution (P.M.F.)
- Variance of Binomial Distribution (P.M.F.)
- Poisson Distribution
- Expected Value and Variance of a Random Variable
Continuity
Differentiation
Applications of Derivative
Indefinite Integration
- Definition of an Integral
- Integral of Standard Functions
- Rules of Integration
- Methods of Integration
- Integration by Parts
Definite Integrals
Ratio, Proportion and Partnership
Commission, Brokerage and Discount
Insurance and Annuity
- Insurance and Annuity
Demography
- Concept of Demography
- Uses of Vital Statistics in Demography
- Measurements of Mortality
- Life Tables
Bivariate Data and Correlation
Regression Analysis Introduction
- Lines of Regression of X on Y and Y on X Or Equation of Line of Regression
- Regression Coefficient of X on Y and Y on X
- Regression Propertise
Random Variable and Probability Distribution
Management Mathematics
- Inequations in Management Mathematics
- Linear Programming Problem in Management Mathematics
- Assignment Problem
- Sequencing in Management Mathematics
- Simple curves: lines, parabolas, polynomial functions
Notes
We consider the easy way of finding the area bounded by the curve y = f(x), x-axis and the ordinates x = a and x = b. Fig.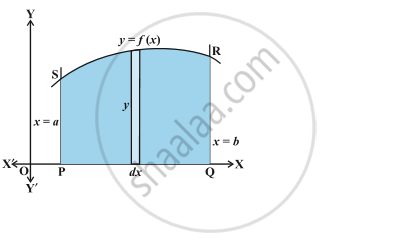
The area under the curve as composed of large number of very thin vertical strips. Consider an arbitrary strip of height y and width dx, then dA (area of the elementary strip)= ydx, where, y = f(x).
This area is called the elementary area which is located at an arbitrary position within the region which is specified by some value of x between a and b. The total area A of the region between x-axis, ordinates x = a, x = b and the curve y = f (x) as the result of adding up the elementary areas of thin strips across the region PQRSP. Symbolically, we express
A = `int_a^b dA = int_a^b ydx = int_a^b f(x) dx`
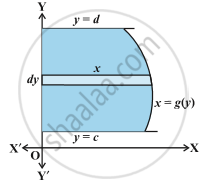
The area A of the region bounded by the curve x = g (y), y-axis and the lines y = c, y = d is given by
A = `int_c^d x dy = int_c^d g(y) dy`
we consider horizontal strips as shown in the following Fig.
Remark: If the position of the curve under consideration is below the x-axis, then since f (x) < 0 from x = a to x = b, as shown in following Fig .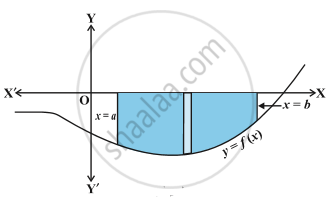
The area bounded by the curve, x-axis and the ordinates x = a, x = b come out to be negative. But, it is only the numerical value of the area which is taken into consideration. Thus, if the area is negative, we take its absolute value, i.e., `|int_a^b f(x) dx|`.
Generally, it may happen that some portion of the curve is above x-axis and some is below the x-axis as shown in the following Fig .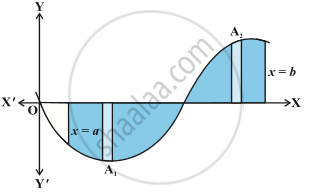
Here , `A_1` < 0 and `A_2`> 0.Therefore, the area A bounded by the curve y = f (x), x-axis and the ordinates x = a and x = b is given by A = |`A_1`|+`A_2`.
