Advertisements
Advertisements
प्रश्न
The area of a rectangle is x2 + 7x + 12. If its breadth is (x + 3), then find its length
उत्तर
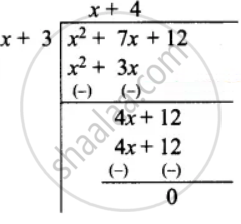
Let the length of the rectangle be “l”
The breadth of the rectangle = x + 3
Area of the rectangle = length × breadth
x2 + 7x + 12 = l(x + 3)
l =
=
= x + 4
Length of the rectangle = x + 4
APPEARS IN
संबंधित प्रश्न
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial
x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial
x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm
deg q(x) = deg r(x)
Apply division algorithm to find the quotient q(x) and remainder r(x) on dividing f(x) by g(x) in the following f(x) = x3 − 6x2 + 11x − 6, g(x) = x2 + x + 1
Apply division algorithm to find the quotient q(x) and remainder r(x) on dividing f(x) by g(x) in the following f(x) = 4x3 + 8x2 + 8x + 7, g(x) = 2x2 − x + 1
Obtain all zeros of the polynomial f(x) = x4 − 3x3 − x2 + 9x − 6, if two of its zeros are
Find the quotient and remainder of the following.
(8y3 – 16y2 + 16y – 15) ÷ (2y – 1)
Find the quotient and remainder of the following.
(8x3 – 1) ÷ (2x – 1)
Find k so that x2 + 2x + k is a factor of 2x4 + x3 – 14 x2 + 5x + 6. Also find all the zeroes of the two polynomials.
Given that
