Advertisements
Advertisements
प्रश्न
The area of a trapezium is 1586 cm2 and the distance between the parallel sides is 26 cm. If one of the parallel sides is 38 cm, find the other.
उत्तर
Area of the trapezium = 1586 cm2
Distance between the parallel sides = 26 cm
And, length of one parallel side = 38 cm
Let us suppose the length of the other side to be x cm .
Now, area of the trapezium \[=\frac{1}{2}\times(\text{ Sum of the parallel sides })\times(\text{ Distance between the parallel sides })\]
\[ \Rightarrow 1586 =\frac{1}{2}\times(38+x)\times(26)\]
\[ \Rightarrow 1586=\frac{26}{2}\times(38+x)\]
\[ \Rightarrow 13\times(38+x)=1586\]
\[ \Rightarrow 38+x = \frac{1586}{13}=122\]
\[ \Rightarrow x = 122-38=84 cm\]
Hence, the length of the other parallel side is 84 cm.
APPEARS IN
संबंधित प्रश्न
Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.

Find the area, in square metres, of the trapezium whose bases and altitude is as under:
bases = 28 cm and 3 dm, altitude = 25 cm
Find the altitude of a trapezium whose area is 65 cm2 and whose bases are 13 cm and 26 cm.
Top surface of a table is trapezium in shape. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.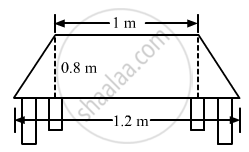
Find the area of the pentagon shown in fig. 20.48, if AD = 10 cm, AG = 8 cm, AH = 6 cm, AF = 5 cm, BF = 5 cm, CG = 7 cm and EH = 3 cm.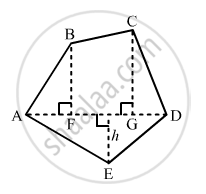
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm respectively and its height is 4.2 cm, find its area.
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 10 m | 12 m | 20 m |
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 13 cm | 28 cm | 492 sq.cm |
When the non-parallel sides of a trapezium are equal then it is known as
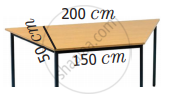
The table top is in the shape of a trapezium with measurements given in the figure. Find the cost of the glass used to cover the table at the rate of ₹ 6 per 10 sq.cm