Advertisements
Advertisements
प्रश्न
The circuit diagram given below shows the combination of three resistors R1, R2 and R3:

Find :
(i) total resistance of the circuit.
(ii) total current flowing in the circuit.
(iii) the potential difference across R1.
उत्तर
(i) As shown in the figure, the resistors R2 and R3 are connected in parallel. Their total resistance is given by:
1/R = 1/R2+ 1/R3
Here, R2 = 3 Ω
R3 = 6 Ω
So,
1/R = 1/3 + 1/6
Or 1/R = (2+1)/6
1/R = 3/6
R = 2 Ω
This resistance is in series with the resistor, R1.
Total resistance = 2 Ω + R1
R1 = 4 Ω
Therefore, total resistance = 2 Ω + 4 Ω = 6 Ω
(ii) The current through the circuit can be calculated as follows:
Current, I = V / R
I = (12 / 6) A
I = 2 A
(iii) The potential difference across R1 = 2 A x 4 Ω = 8 V
APPEARS IN
संबंधित प्रश्न
Fill in the folloing blank with suitable words:
A current is a flow of ............... .For this to happen there must be a ............... circuit.
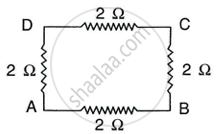
In the network shown in the following adjacent Figure, calculate the equivalent resistance between the points.
- A and B
- A and C
State the relation between work, charge and potential difference for an electric circuit.
A bulb marked 12 V, 24 W operates on a 12 volt car battery for 20 minutes. Calculate:
(i) The current flowing through it, and
(ii) The energy liberated.
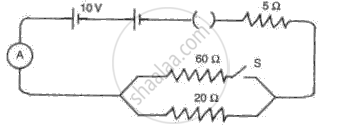
In the circuit shown in fig. 6, find the reading of the ammeter A when the switch S is
(a) Opened.
(b) Closed.
In a house there are 6 bulbs of 100 W each used for 4 hours a day, 4 bulbs of 60 W each used for 8 hours a day, an immersion heater of 2.5 kW used for 1 hour per day, and an electric iron of 800 W used for 2 hours per day. Calculate the cost of monthly electric bill for the month of April at the rate of 80 p per unit.
An auto lamp is joined to a battery of e.m.f. 4 V and internal resistance 2.5Ω. A steady current of 0.5 A flows through the circuit. Calculate the
(a) Total energy provided by battery in 10 minutes,
(b) Heat dissipated in the bulb in 10 minutes.
One unit of electrical energy consumed is equal to 1000 kilowatt-hour.
