Advertisements
Advertisements
प्रश्न
The constant A in the Richardson−Dushman equation for tungsten is 60 × 104 A m−2K−2. The work function of tungsten is 4.5 eV. A tungsten cathode with a surface area 2.0 × 10−5 m2 is heated by a 24 W electric heater. In steady state, the heat radiated by the heater and the cathode equals the energy input by the heater and the temperature becomes constant. Assuming that the cathode radiates like a blackbody, calculate the saturation current due to thermions. Take Stefan's Constant = 6 × 10−8 W m−2 K−1. Assume that the thermions take only a small fraction of the heat supplied.
उत्तर
Given:-
A = 60 × 104 A m−2 K−2
Work function of tungsten, ϕ = 4.5 eV
Stefan's Constant, σ = 6 × 10−8 W m−2 K−1
Surface area of tungsten cathode, S = 2.0 × 10−5 m2
Boltzmann's Constant, k = 1.38× 10−23 J/K
Heat supplied by the heater, H = 24 W
The cathode acts as a black body; thus, its emissivity is 1.
According Stefan's Law:-
The power (P) radiated by a blackbody with surface area (A) and temperature (T),
\[P = \sigma A T^4 \]
\[ \Rightarrow T^4 = \frac{P}{\sigma A}\]
\[ \Rightarrow T^4 = \frac{24}{(6 \times {10}^{- 8} ) \times (2 \times {10}^{- 5} )}\]
\[ \Rightarrow T^4 = 2 \times {10}^{13} K = 20 \times {10}^{12} K\]
\[ \Rightarrow T = 2 . 1147 \times {10}^3 = 2114 . 7 K\]
According to the Richard-Dushmann equation, emission current,
\[i = AS T^2 e^{- \phi/KT} \]
\[i = 6 \times {10}^5 \times 2 \times {10}^{- 5} \times (2114 . 7 )^2 \times e^\frac{- 4 . 5 \times 1 . 6 \times {10}^{- 19}}{1 . 38 \times {10}^{- 23} \times 2114 . 7} \]
\[i = 1 . 03456 \times {10}^{- 3} A \approx 1 . 0\text{ mA}\]
APPEARS IN
संबंधित प्रश्न
The work function of caesium metal is 2.14 eV. When light of frequency 6 × 1014 Hz is incident on the metal surface, photoemission of electrons occurs. What is the
- maximum kinetic energy of the emitted electrons,
- Stopping potential, and
- maximum speed of the emitted photoelectrons?
Quarks inside protons and neutrons are thought to carry fractional charges [(+2/3)e; (–1/3)e]. Why do they not show up in Millikan’s oil-drop experiment?
How does one explain the emission of electrons from a photosensitive surface with the help of Einstein's photoelectric equation?
Would you prefer a material with a high melting point or a low melting point to be used as a cathode in a diode?
A diode value is connected to a battery and a load resistance. The filament is heated, so that a constant current is obtained in the circuit. As the cathode continuously emits electrons, does it become more and more positively charged?
Why does thermionic emission not take place in non-conductors?
The cathode of a diode valve is replaced by another cathode of double the surface area. Keeping the voltage and temperature conditions the same, will the place current decrease, increase or remain the same?
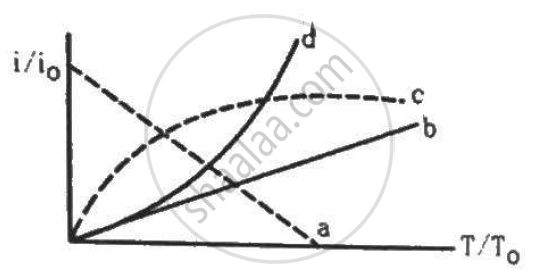
Let i0 be the thermionic current from a metal surface when the absolute temperature of the surface is T0. The temperature is slowly increased and the thermionic current is measured as a function of temperature. Which of the following plots may represent the variation in (i/i0) against (T/T0)?
The anode of a thermionic diode is connected to the negative terminal of a battery and the cathode to its positive terminal.
Define the term "Threshold frequency", in the context of photoelectric emission.
The work function of aluminum is 4⋅2 eV. If two photons each of energy 2⋅5 eV are incident on its surface, will the emission of electrons take place? Justify your answer.
The wavelength λe of an electron and λp of a photon of same energy E are related by
The wave associated with a moving particle of mass 3 × 10–6 g has the same wavelength as an electron moving with a velocity 6 × 106 ms–1. The velocity of the particle is
Emission of electrons by the absorption of heat energy is called ____________ emission.
Why do metals have a large number of free electrons?
What do you mean by electron emission? Explain briefly various methods of electron emission.
A 150 W lamp emits light of the mean wavelength of 5500 Å. If the efficiency is 12%, find out the number of photons emitted by the lamp in one second.
