Advertisements
Advertisements
प्रश्न
The current in a long solenoid of radius R and having n turns per unit length is given by i= i0 sin ωt. A coil having N turns is wound around it near the centre. Find (a) the induced emf in the coil and (b) the mutual inductance between the solenoid ant the coil.
उत्तर
Given:-
Radius of the long solenoid = R
Number of turns per unit length of the long solenoid = n
Current in the long solenoid, i = i0 sin ωt
Number of turns in the small solenoid = N
Radius of the small solenoid = R
The magnetic field inside the long solenoid is given by
B = μ0ni
Flux produced in the small solenoid because of the long solenoid, ϕ = (μ0ni) × (NπR2)
(a) The emf developed in the small solenoid is given by
\[e =\frac{d\phi}{dt} = \frac{d}{dt}( \mu_0 niN\pi R^2 )\]
`e = μ_0nN πR^2(di)/(dt)`
Substituting i = i0 sin ωt, we get
e = μ0nNπR2i0ω cos ωt
(b) Let the mutual inductance of the coils be m.
Flux ϕ linked with the second coil is given by
ϕ = (μ0 ni) × (NπR2)
The flux can also be written as
ϕ = mi
∴ (μ0 ni) × (NπR2) = mi
And,
m = πμ0nNR2
APPEARS IN
संबंधित प्रश्न
The co-efficient of mutual induction between primary and secondary coil is 2H. Calculate induced e.m.f. if current of 4A is cut off in 2.5 x 10-4 seconds
Define mutual inductance.
Define mutual inductance.
A coil of self-inductance 2.5H and resistance 20Ω is connected to a battery of emf 120V having the internal resistance of 5 n. Find:
1) The time constant of the circuit.
2) The current in the circuit in steady state
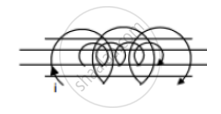
Find the mutual inductance between the circular coil and the loop shown in figure.
A solenoid of length 20 cm, area of cross-section 4.0 cm2 and having 4000 turns is placed inside another solenoid of 2000 turns having a cross-sectional area 8.0 cm2 and length 10 cm. Find the mutual inductance between the solenoids.
A pair of the adjacent coil has a mutual inductance of 1.5 H. If the current in one coil varies from 0 to 20 A in 0.5 s, what is the change of flux linked with the other coil.
Define Mutual Inductance.
The dimensions of self or mutual inductance are given as ______.
Two coils are placed close to each other. The mutual inductance of the pair of coils depends upon the ______.
Two circular coils have their centres at the same point. The mutual inductance between them will be maximum when their axes ______
Two conducting circular loops of radii R1 and R2 are placed in the same plane with their centres coinciding. If R1 > > R2, the mutual inductance M between them will be directly proportional to ______.
The mutual inductance M12 of coil 1 with respect to coil 2 ______.
- increases when they are brought nearer.
- depends on the current passing through the coils.
- increases when one of them is rotated about an axis.
- is the same as M21 of coil 2 with respect to coil 1.
Write the S.I. unit of mutual inductance.
A rectangular coil of wire 50 turn each of area 6 x 10-4 m2 is freely suspended in a field of 3 x 10-2 Wb / m2. Calculate the current flowing through the coil when it deflects through 60°, when torsional constant is 3.82 x 10-6 SI unit.
State and define the SI unit of mutual inductance.
Two coils having self inductances L1 = 75 mH and L2 = 55 mH are coupled with each other. The coefficient of coupling (K) is 0. 75. Calculate the mutual inductance (M) of the two coils
