Advertisements
Advertisements
प्रश्न
The decimal expansion of the rational number \[\frac{43}{2^4 \times 5^3}\] will terminate after how many places of decimals?
उत्तर
We have,
`43/(2^4xx5^3)`
Theorem states:
Let `x= p/q` be a rational number, such that the prime factorization of q is of the form `2^nxx 5^m`, where mand n are non-negative integers.
Then, x has a decimal expression which terminates after k places of decimals, where k is the larger of mand n.
This is clear that the prime factorization of the denominator is of the form `2^nxx 5^m`,.
Hence, it has terminating decimal expansion which terminates after 4 places of decimal.
APPEARS IN
संबंधित प्रश्न
If the rational number `a/b`has a terminating decimal expansion, what is the condition to be satisfied by b?
Write the decimal expansion of `73/ ((2^4×5^3))`
Express 0.`bar (23)` as a rational number in simplest form.
Write a rational number between`sqrt(3)` and 2
Without actually performing the long division, state whether state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion.
Write down the decimal expansions of the following rational numbers by writing their denominators in the form 2m × 5n, where, m, n are non-negative integers.\[\frac{14588}{625}\]
Complete the missing entries in the following factor tree.
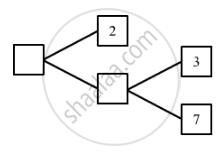
Write down the decimal expansion of the following number which have terminating decimal expansion.
`64/455`
Write down the decimal expansion of the following number which have terminating decimal expansion.
`129/(2^2xx5^7xx7^5)`
The smallest number by which `1/13` should be multiplied so that its decimal expansion terminates after two decimal places is ______.
