Advertisements
Advertisements
प्रश्न
The difference between the measures of the two angles of a complementary pair is 40°. Find the measures of the two angles.
उत्तर १
Let the measure of the first angle x.
Then, the measure of the other angle x + 40°
Now, x° + (x + 40)° = 90° ...(Since, the two angles are complementary)
∴ 2x° + 40° − 40° = 90° − 40 ...(Subtracting 40 from both sides)
∴ 2x° = 50°
∴ `x^circ = 50/2`
∴ x° = 25°
∴ x + 40°
= 25° + 40°
= 65°
Hence, the measures of the two angles are 25° and 65°.
उत्तर २
Step 1: Use the definition of complementary angles
x + y = 90∘
Step 2: Use the given difference between the angles
x − y = 40∘
Step 3: Solve the system of equations
We have:
- x + y = 90°
- x − y = 40°
Add the two equations:
(x + y) + (x − y) = 90° + 40°
2x° = 130°
x° = 65∘
Substitute x = 65° into the first equation:
65° + y = 90°
y = 25°
The two angles are 65° and 25°.
संबंधित प्रश्न
Find the supplement of the following angle:

Identify the given pair of angles are complementary or supplementary.
130°, 50°
Find the angle which is equal to its supplement.
Find the supplementary angle of 0°
If angle P and angle Q are supplementary and the measure of angle P is 60°, then the measure of angle Q is ______.
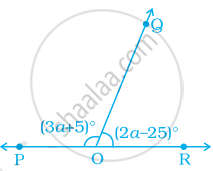
In the given figure, POR is a line. The value of a is ______.
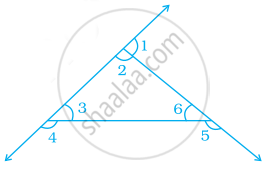
Name the pairs of supplementary angles in the following figure:
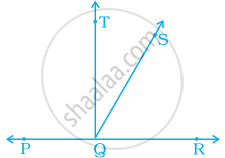
In the given figure, P, Q and R are collinear points and TQ ⊥ PR, name; two pairs of supplementary angles.
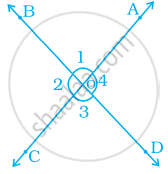
If two angles have a common vertex and their arms form opposite rays (Figure), Then, how many types of angles are formed?
Can two acute angles form a pair of supplementary angles? Give reason in support of your answer.
