Advertisements
Advertisements
Question
The difference between the measures of the two angles of a complementary pair is 40°. Find the measures of the two angles.
Solution 1
Let the measure of the first angle x.
Then, the measure of the other angle x + 40°
Now, x° + (x + 40)° = 90° ...(Since, the two angles are complementary)
∴ 2x° + 40° − 40° = 90° − 40 ...(Subtracting 40 from both sides)
∴ 2x° = 50°
∴ `x^circ = 50/2`
∴ x° = 25°
∴ x + 40°
= 25° + 40°
= 65°
Hence, the measures of the two angles are 25° and 65°.
Solution 2
Step 1: Use the definition of complementary angles
x + y = 90∘
Step 2: Use the given difference between the angles
x − y = 40∘
Step 3: Solve the system of equations
We have:
- x + y = 90°
- x − y = 40°
Add the two equations:
(x + y) + (x − y) = 90° + 40°
2x° = 130°
x° = 65∘
Substitute x = 65° into the first equation:
65° + y = 90°
y = 25°
The two angles are 65° and 25°.
RELATED QUESTIONS
In the given figure, ∠1 and ∠2 are supplementary angles.
If ∠1 is decreased, what changes should take place in ∠2 so that both the angles still remain supplementary.
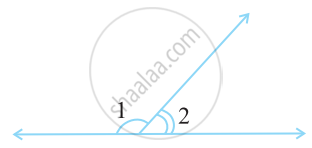
Can two angles be supplementary if both of them are acute?
If two angles are supplementary, then the sum of their measures is _______.
What will be the measure of the supplement of the following angles?
55º
Find the supplementary angle of 165°
Find the supplementary/complementary angle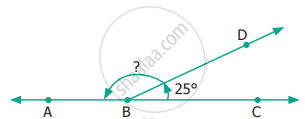
The supplement of a right angle is always ______ angle.
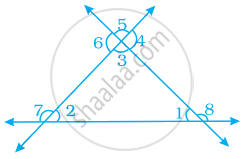
Name the pairs of supplementary angles in the following figure:
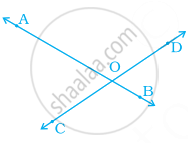
If two angles have a common vertex and their arms form opposite rays (Figure), Then, how many types of angles are formed?
In the given figure, write all the pairs of supplementary angles.