Advertisements
Advertisements
Question
In ∆XYZ, m∠Y = 90°. What kind of a pair do ∠X and ∠Z make?
Solution
In ∆XYZ,
∠X + ∠Y + ∠Z = 180° ...(Angle Sum property of triangle)
⇒ ∠X + 90° + ∠Z = 180°
∴ m∠X + 90° + m∠Z – 90° = 180° – 90° ...(Subtracting 90 from both sides)
⇒ ∠X + ∠Z = 90°
Since, the sum of the measures of the two angles is 90°.
Hence, ∠X and ∠Z are complementary angles.
RELATED QUESTIONS
Identify the given pair of angles are complementary or supplementary.
65°, 115°
In the given figure, ∠1 and ∠2 are supplementary angles.
If ∠1 is decreased, what changes should take place in ∠2 so that both the angles still remain supplementary.
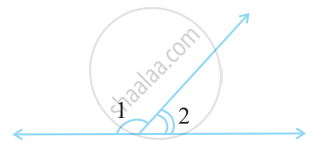
If two angles are supplementary, then the sum of their measures is _______.
Write the measure of the supplement of the angle given below.
120°
What will be the measure of the supplement of the following angles?
55º
Among two supplementary angles, the measure of the larger angle is 44o more than the measure of the smaller. Find their measures.
From the figure given below, classify the following pair of angles into supplementary and non supplementary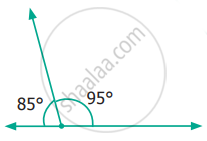
If angle P and angle Q are supplementary and the measure of angle P is 60°, then the measure of angle Q is ______.
If two angles have a common vertex and their arms form opposite rays (Figure), Then, how many types of angles are formed?