Advertisements
Advertisements
प्रश्न
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ₹ 10 per m2 is ₹ 15,000, find the height of the hall.
उत्तर
Let the length, breadth, and height of the rectangular hall be l m, b m, and h m respectively.
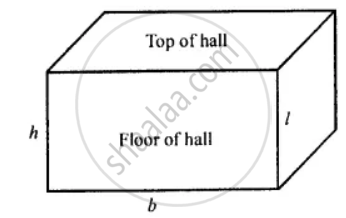
The perimeter of the floor of hall = 2(l + b)
250 m = 2(l + b)
(l + b) = `250/2 = 125` cm ...(i)
Area of four walls = Area of cuboid – Area of floor – Area of top
= 2 (lb + bh + hl) – (l x b) – (l x b)
= 2(lb) + 2 (bh) + 2(hl) – 2lb = 2 lh + 2 bh
= 2h(l + b)
= 2h x 125 [From (i)]
= 250h m2
Area of four walls = 250h m2
Cost of painting 1 m2 area = ₹ 10
Cost of painting 250h m2 area = ₹ 10 x 250h = 2500h
15000 = 2500h
h = `15000/2500`
The height of the hall is 6 m.
APPEARS IN
संबंधित प्रश्न
The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of Rs 7.50 per m2.
There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
 |
 |
| (a) | (b) |
Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth, and height of 15 m, 10 m, and 7 m, respectively. From each can of paint, 100 m2 of area is painted. How many cans of paint will she need to paint the room?
The dimensions of a rectangular box are in the ratio of 2 : 3 : 4 and the difference between the cost ofcovering it with sheet of paper at the rates of Rs. 8 and Rs. 9.50 per m2 is Rs.1248. Find the dimensions of the box.
The length and breadth of a hall are in the ratio 4: 3 and its height is 5.5 metres. The cost of decorating its walls (including doors and windows) at Rs. 6.60 per square metre is Rs. 5082. Find the length and breadth of the room.
How many wooden cubical blocks of side 25 cm can be cut from a log of wood of size 3 m by 75 cm by 50 cm, assuming that there is no wastage?
How much clay is dug out in digging a well measuring 3 m by 2 m by 5 m?
A village, having a population of 4000, requires 150 litres water per head per day. It has a tank which is 20 m long, 15 m broad and 6 m high. For how many days will the water of this tank last?
A cuboidal box is 5 cm by 5 cm by 4 cm. Find its surface area.
A cloassroom is 11 m long, 8 m wide and 5 m high. Find the sum of the areas of its floor and the four walls (including doors, windows, etc.)
The central hall of a school is 80 m long and 8 m high. It has 10 doors each of size 3 m × 1.5 m and 10 windows each of size 1.5 m × 1 m. If the cost of white-washing the walls of the hall at the rate of Rs 1.20 per m2 is Rs 2385.60, fidn the breadth of the hall.
The breadth of a room is twice its height, one half of its length and the volume of the room is 512 cu. dm. Find its dimensions.
The dimensions of a cinema hall are 100 m, 50 m and 18 m. How many persons can sit in the hall, if each person requires 150 m3 of air?
If the length of a diagonal of a cube is `8 sqrt(3)` cm, then its surface area is
If the areas of the adjacent faces of a rectangular block are in the ratio 2 : 3 : 4 and its volume is 9000 cm3, then the length of the shortest edge is
Volume of a cuboid is 12 cm3. The volume (in cm3) of a cuboid whose sides are double of the above cuboid is
The sum of the length, breadth and depth of a cuboid is 19 cm and its diagonal is ` 5 sqrt(5)` cm. Its surface area is
If each edge of a cube is increased by 50%, the percentage increase in its surface area is
The dimensions of a Cinema Hall are 100 m, 60 m, and 15 m. How many persons can sit in the hall if each requires 150 m3 of air?
Find the volume and the total surface area of a cuboid, whose :
length = 15 cm, breadth = 10 cm and height = 8 cm.
How many persons can be accommodated in a big-hall of dimensions 40 m, 25 m, and 15 m; assuming that each person requires 5 m3 of air?
A closed box measures 66 cm, 36 cm and 21 cm from outside. If its walls are made of metal-sheet, 0.5 cm thick; find :
(i) the capacity of the box ;
(ii) the volume of metal-sheet and
(iii) weight of the box, if 1 cm3 of metal weighs 3.6 gm.
The length, breadth, and height of a cuboid (rectangular solid) are 4 : 3: 2.
(i) If its surface area is 2548 cm2, find its volume.
(ii) If its volume is 3000 m3, find its surface area.
Find the capacity of a cylindrical container with an internal diameter of 28 cm and a height of 20 cm.
The diameter of a garden roller is 1.4 m and it 2 m long. Find the maximum area covered by its 50 revolutions?
Find the volume of a cuboid whose diagonal is `3sqrt(29)"cm"` when its length, breadth and height are in the ratio 2 : 3 : 4.
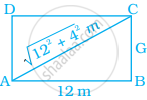
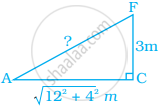
Find the length of the largest pole that can be placed in a room of dimensions 12 m × 4 m × 3 m.