Question

The locus of the midpoints of the chord of the circle, x² + y² = 25 which is tangent to the hyperbola, `x^2/9 - y^2/16` = 1 is ______.

विकल्प

• (x² + y²)² – 16x² + 9y² = 0

• (x² + y²)² – 9x² + 144y² = 0

• (x² + y²)² – 9x² – 16y² = 0

• (x² + y²)² – 9x² + 16y² = 0

Answer 1

The locus of the midpoints of the chord of the circle, x² + y² = 25 which is tangent to the hyperbola, `x^2/9 - y^2/16` = 1 is `underlinebb((x^2 + y^2)^2 –  9x^2 + 16y^2 = 0)`.

Explanation:

Given equation of circle is x² + y² = 25

C(0, 0) and radius r = 5

Let the mid pint of the chord of the circle x² + y² = 25 be M(h, k)

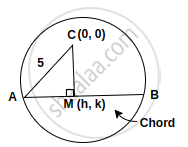
In the above figure

AM = MB and AC = 5 (radius)

Slope of MC, m_MC = `("k" - 0)/("h" - 0)`

⇒ m_MC = `"k"/"h"`

Let the slope of AB be m_AB

Then, m_AB.m_MC = –1  ...[∵ MC ⊥ AB]

m_AB = `(-"h")/"k"`

Equation of chord AB

y – k = m_AB(x – h)

⇒ y – k = `(-h)/k(x - h)`

⇒ ky = –hx + h² + k²

⇒ y = `((-"h")/"k")x + (("h"^2 + "k"^2)/"k")`  ...(i)

Since, the equation (i) is the tangent to the hyperbola `x^2/9 - "y"^2/16` = 1  ...(ii)

If y = mx + c is tangent to the hyperbola `x^2/a^2 - "y"^2/"b"^2` = 1, (a < b) then c² = a²m² – b²

From equation (i) and (ii),

`(("h"^2 + "k"^2)/"k")^2 = (9)((-"h")/"k") - (16)`

⇒ `(("h"^2 + "k"^2)/"k")^2 = (9"h"^2 - 16"k"^2)/"k"^2`

⇒ (h² + k²) = 9h² – 16h²

Replace h and k by x and y

(x² + y²)² = 9x² – 16y²

(x² + y²)² = 9x² + 16y² = 0