Advertisements
Advertisements
प्रश्न
The motion of a particle executing simple harmonic motion is described by the displacement function,
x (t) = A cos (ωt + φ).
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle? The angular frequency of the particle is π s–1. If instead of the cosine function, we choose the sine function to describe the SHM: x = B sin (ωt + α), what are the amplitude and initial phase of the particle with the above initial conditions.
उत्तर १
Initially, at t = 0:
Displacement, x = 1 cm
Initial velocity, v = ω cm/sec.
Angular frequency, ω = π rad/s–1
It is given that:
`x(t) = A cos(omegat + phi)`
`1 = A cos(omega xx 0 xx phi)`
`A cos phi = 1` ....(i)
`"Velocity", v = (dx)/(dt)`
`omega = - Aomegasin(omegat + phi)`
`1 = -A sin (omega xx 0 + phi)` = `- A Sin phi`
`Asin phi = -1` ...(ii)
Squaring and adding equations (i) and (ii), we get:
`A^2(sin^2 phi + cos^2 phi) = 1+ 1`
`A^2= 2`
`:. A = sqrt2 cm`
Dividing equation (ii) by equation (i), we get:
`tan phi = -1`
`: phi = (3pi)/4, (7pi)/4,....`
SHM is given as:
`x = B sin(omegat + alpha)`
Putting the given values in this equation, we get:
`1 = B sin[omegaxx0 + alpha]`
`B sin alpha = 1` ....(iii)
Velocity, `v = omegaBcos(omegat + alpha)`
Substituting the given values, we get:
`pi = piBsin alpha`
`Bsin alpha = 1` .....(iv)
Squaring and adding equations (iii) and (iv), we get:
`B^2[sin^2alpha + cos^2 alpha] = 1+ 1`
`B^2 = 2`
`:. B = sqrt2 cm`
Dividing equation (iii) by equation (iv), we get:
`(Bsin alpha)/(B cos alpha) = 1/1`
`tan alpha = 1 = tan pi/4`
`:. alpha = pi/4 , (5pi)/4, ......`
उत्तर २
The given displacement function is
`x(t) = A cos (omegat + phi)` ....(i)
At t = 0, x(0) = 1 cm,Also `omega = pis^(-1)`
`:. 1 = A cos (pi xx 0 +phi)`
`=> A cos phi = 1`
Also, differentiating equation (i) w.r.t 't'
`v= d/(dt) x(t ) = -A omega sin (omegat + phi)`
Now at t = 0, `v = omega`
:. From equation (iii) `omega = -A omega sin (pi xx0+ phi)` or `A sinphi = -1`
Squaring and adding eqations (ii) and (iv)
`A^2 cos^2phi + A^2 sin^2 phi = 1^2 + 1^2` or `A = sqrt2 cm`
Dividing equation (ii) and (iv)
`(A sin phi)/(A cos phi) = (-1)/1`
`:. tan phi = -1 => phi = (3pi)/4`
If instead we use the sine function, i.e
`x = Bsin (omegat + alpha)` ,then `v = d/(dt) B omega cos (omegat + alpha)`
:. At t = 0 using x= 1 and `v = omega`, we get `1 = B sin(omega xx 0 + alpha)`
or `B sin alpha = 1` ....(v)
and `omega = Bomega cos (omega xx 0 + alpha)` or `B cos alpha = 1` ...(vi)
Dividing v and vi
`tan alpha = 1 or alpha = pi/4 or (5pi)/4`
Squaring v and vi, we get
`B^2 sin^2 alpha + B^2 cos^2 alpha = 1^2 + 1^2`
`=> B = sqrt2 cm`
APPEARS IN
संबंधित प्रश्न
Figures correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure

Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
Figure (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure (b) shows the same spring with both ends free and attached to a mass mat either end. Each end of the spring in Fig. (b) is stretched by the same force F.
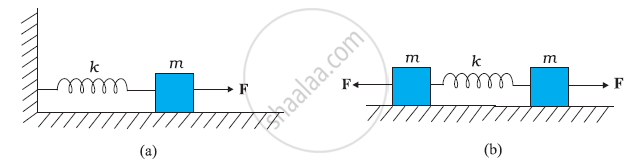
(a) What is the maximum extension of the spring in the two cases?
(b) If the mass in Fig. (a) and the two masses in Fig. (b) are released, what is the period of oscillation in each case?
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):
sin ωt – cos ωt
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):
sin3 ωt
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):
3 cos `(π/4 – 2ω"t")`
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):
cos ωt + cos 3ωt + cos 5ωt
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):
exp (–ω2t2)
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):
1 + ωt + ω2t2
A particle is acted simultaneously by mutually perpendicular simple harmonic motions x = a cos ωt and y = a sin ωt. The trajectory of motion of the particle will be ______.
The rotation of earth about its axis is ______.
- periodic motion.
- simple harmonic motion.
- periodic but not simple harmonic motion.
- non-periodic motion.
