Advertisements
Advertisements
प्रश्न
The number of diagonals of an n-sided figure is `1/2(n^2 - 3n)`. Use the formula to find the number of diagonals for a 6-sided figure (hexagon).
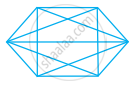
उत्तर
Given, a polygon has n sides, then number of diagonals is `1/2(n^2 - 3n)`
In hexagon, there are six sides
Therefore for calculating number of diagonals in hexagon, put n = 6 in the above formula
∴ Number of diagonals = `1/2[n^2 - 3n]`
= `1/2(6^2 - 3 xx 6)`
= `1/2(6 xx 6 - 3 xx 6)`
= `1/2(36 - 18)`
= `1/2(18)`
= 9
Hence, a hexagon has 9 diagonals.
APPEARS IN
संबंधित प्रश्न
Express the following as product of powers of its prime factor:
405
Evaluate: `(- 5/6)^5`
Which is greater:
54 or 45
Complete the table below.
| Sr. No | Indices (Numbers in index form) |
Base | Index | Multiplication form | Value |
| (i) | 34 | 3 | 4 | 3 × 3 × 3 × 3 | 81 |
| (ii) | 163 | ||||
| (iii) | (−8) | 2 | |||
| (iv) | `3/7 xx 3/7 xx 3/7 xx 3/7` | `81/2401` | |||
| (v) | (−13)4 |
Expand a3b2, a2b3, b2a3, b3a2. Are they all same?
Fill in the blanks with <, > or = sign
32 ______ 15
49 is greater than 163.
Express the following in exponential form:
a × a × b × b × b × c × c × c × c
Write the number of seconds in scientific notation.
| Sl. No. | Unit | Value in Seconds |
| 1. | 1 Minute | 60 |
| 2. | 1 Hour | 3,600 |
| 3. | 1 Day | 86,400 |
| 4. | 1 Month | 2,600,000 |
| 5. | 1 Year | 32,000,000 |
| 6. | 10 Years | 3,20,000,000 |
