Advertisements
Advertisements
Question
The number of diagonals of an n-sided figure is `1/2(n^2 - 3n)`. Use the formula to find the number of diagonals for a 6-sided figure (hexagon).
Advertisements
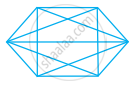
Solution
Given, a polygon has n sides, then number of diagonals is `1/2(n^2 - 3n)`.
In hexagon, there are six sides
Therefore for calculating number of diagonals in hexagon, put n = 6 in the above formula
∴ Number of diagonals = `1/2[n^2 - 3n]`
= `1/2(6^2 - 3 xx 6)`
= `1/2(6 xx 6 - 3 xx 6)`
= `1/2(36 - 18)`
= `1/2(18)`
= 9
Hence, a hexagon has 9 diagonals.
APPEARS IN
RELATED QUESTIONS
Express the following in exponential form:
2 × 2 × a × a
Identify the greater number, wherever possible, in the following?
28 or 82
Simplify:
72 × 22
Evaluate:
`[(1/4)^-3-(1/3)^-3]÷(1/6)^-3`
Which one is greater 23 or 32?
Expand a3b2, a2b3, b2a3, b3a2. Are they all same?
Find the value of the following.
93
Express the following in exponential form:
3 × 3 × 3 × a × a × a × a
Identify the greater number in the following:
26 or 62
