Question

The number of elements in the set {x ∈ R: (|x| –3)|x + 4| = 6} is equal to ______.

विकल्प

• 2

• 1

• 3

• 4

Answer 1

The number of elements in the set {x ∈ R: (|x| –3)|x + 4| = 6} is equal to 2.

Explanation:

Given,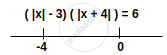

Case I: when x < – 4

Since, |x| = `{{:(x; x > 0),(-x; x < 0):}`

⇒ (–x – 3)(–x – 4) = 6

⇒ (x + 3)(x + 4) = 6

⇒ x² + 7x + 6 = 0

⇒ (x + 6)(x + 1) = 0

⇒ x = –1 and –6

As x < –4 so for this case x = {–6}

Case II: when x ∈ [–4, 0)

Using |x| = `{{:(x; x ≥ 0),(-x; x < 0):}`

(–x – 3)(x + 4) = 6

⇒ x² + 7x + 18 = 0

⇒ No solution (D < 0)

So, for this case x ∈ Φ

Case III: When x ≥ 0

(x – 3)(x + 4) = 6

⇒ x² + x – 18 = 0

⇒ x = `(-1 +- sqrt(1 + 72))/2`

As x ≥  0 so for this case x = `{(sqrt(73) - 1)/2}` So, final solution of the given equation are `x∈{-6(sqrt(73) - 1)/2}` Hence number of solution will be 2.