Advertisements
Advertisements
प्रश्न
The roots of the quadratic equation `2x^2-x-6=0`
(a)`-2, 3/2` (b) `2, -3/2`
(c)` -2, 3/2` (d) `2, 3/2`
उत्तर
(b) `2, 3/2`
The given quadratic equation is `2x^2-x-6=0`
`2x^2-x-6=0`
⇒`2x^2-4x+3x-6=0`
⇒`2x(x-2)+3(x-2)=0`
⇒`(x-2) (2x+3)=0`
⇒`x-2=0 or 2x+3=0`
⇒ `x=2 or x=(-3)/2`
Thus, the roots of the given equation are `2 and (-3)/2`
Hence, the correct answer is option B.
APPEARS IN
संबंधित प्रश्न
If one root of the equation` 3x^2-10x+3=0 is 1/3` then the other root is
(a) `-1/3` (b) `1/3` (c)`-3` (d)`3`
If the sum of the roots of a quadratic equation is 6 and their product is 6, the equation is
(a)`x^2-6x+6=0` (b)` x^2+6x+6=0` (c)`x^2-6x-6=0` (d)`x^2+6x+6=0`
If α and β are the roots of the equation `3x^2+8x+2=0` then (1/α+1/β)=?
(a)` -3/8` (b) `2/3` `(c) -4 (d)4`
The roots of the equation 2x^2-6x+7=0 are
(a) real, unequal and rational (b) real, unequal and irrational (c) real and equal (d) imaginary
The Sum of squares of 2 consecutive natural even numbers is 244; find the numbers.
If 3x + 5y = 9 and 5x + 3y = 7 find the value of x + y.
Two water taps together can fill a tank in `1 7/8` hours. The tap with a longer diameter takes 2 hours less than the tap with a smaller one to fill the tank separately. Find the time in which each tap can fill the tank separately.
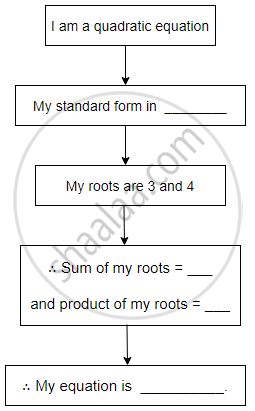
Complete the following activity to form a quadratic equation.
Activity:
The ratio of fruit trees and vegetable trees in an orchard is 3:4. If 6 more trees of each type are planted, the ratio of trees would be 6:7. Find the number of fruit trees and vegetable trees in the orchard.
The ratio of fruit trees and vegetable trees = 3:4
So, let the number of fruit trees= 3x and the number of vegetable trees = `square`
From the given condition,
`(3x + square)/(square + square) = square/square`
`square (3x + square) = square (square + square)`
`square + square = square + square`
`square - square = square - square`
`- square = - square`
`square = square`
x = `square`
∴ Number of fruit trees in the orchard = 3x = 3 × `square` = `square` and number of vegetable trees in the orchard = 4x = 4 × `square` = `square`
Hence, the number of fruit trees and vegetable trees in the orchard are `square` and `square` respectively.
In a right-angled triangle, altitude is 2 cm longer than its base. Find the dimensions of the right-angled triangle given that the length of its hypotenuse is 10 cm.
