Advertisements
Advertisements
प्रश्न
In a right-angled triangle, altitude is 2 cm longer than its base. Find the dimensions of the right-angled triangle given that the length of its hypotenuse is 10 cm.
उत्तर
Let x cm be the base of the right-angled triangle.
As a result, the altitudeude = (x + 2) cm.
Also, hypotenuse = 10 cm
We have the Pythagorean theorem.
(Base)2 + (Altitude)2 = (Hypotenuse)2
⇒ x2 + (x + 2)2 = 102
⇒ x2 + x2 + 4x + 4 = 100
⇒ 2x2 + 4x – 96 = 0
⇒ 2x + 2x – 48 = 0
⇒ x2 + (8 – 6)x – 48 = 0
⇒ x2 + 8x – 6x – 48 = 0
⇒ x(x + 8) – 6(x + 8) = 0
⇒ (x – 6)(x + 8) = 0
⇒ (x + 8) = 0 or (x – 6) = 0
⇒ x = – 8 or x = 6
A triangle's sides cannot be negative.
So, x = 6.
As a result, the right-angled triangle's base is 6 cm and its altitude is 6 + 2 = 8 cm.
As a result, the right-angled triangle's dimensions are 8 cm, 6 cm, and 10 cm.
APPEARS IN
संबंधित प्रश्न
(a) `3x-x^2=x^2+5` (b) `(x+2)^2=2(x^2-5)`
(c) `(sqrt2x+3)^2=2x^2+6` (d)` (x-1)^2=3x^2+x-2`
If the sum of the roots of a quadratic equation is 6 and their product is 6, the equation is
(a)`x^2-6x+6=0` (b)` x^2+6x+6=0` (c)`x^2-6x-6=0` (d)`x^2+6x+6=0`
The roots of `ax^2+bx+c=0`,a≠0 are real and unequal, if `(b^2-4ac)` is
(a)>0 (b)=0 (c)<0 (d)none of these
If the equation `x^2+5kx+16=0` has no real roots then
(a)`k>8/5` (b) `k(-8)/5`
(c)` (-8)/5<k<8/5` (d) None Of these
The perimeter of a rectangle is 82m and its area is `400m^2` . The breadth of the rectangle is
(a) 25m (b)20m
(c) 16m (d)9m
If one zero of the polynomial `x^2-4x+1 is (2+sqrt3)` write the other zero.
Decide whether the following equation is quadratic equation or not.
y2 = 5y – 10
Decide whether the following equation is quadratic equation or not.
(m + 2) (m – 5) = 0
Vivek is older than Kishor by 5 years. The sum of the reciprocals of their ages is \[\frac{1}{6}\] Find their present ages.
Pintu takes 6 days more than those of Nishu to complete certain work. If they work together they finish it in 4 days. How many days would it take to complete the work if they work alone.
Choose the correct answer for the following question.
The roots of x2 + kx + k = 0 are real and equal, find k.
Choose the correct answer for the following question.
Which of the following quadratic equations has roots 3,5?
Find the value of m so that the quadratic equation mx (x − 7) + 49 = 0 has two equal roots.
Two water taps together can fill a tank in `1 7/8` hours. The tap with a longer diameter takes 2 hours less than the tap with a smaller one to fill the tank separately. Find the time in which each tap can fill the tank separately.
Find k, one of the roots of the quadratic equation kx2 - 7x + 12 = 0 is 3.
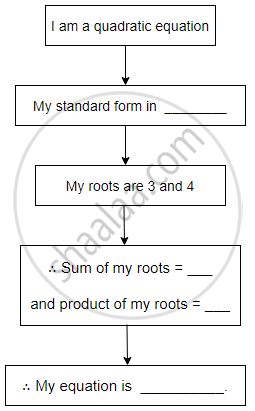
Complete the following activity to form a quadratic equation.
Activity:
Construct a word problem on quadratic equation, such that one of its answers is 20 (years, rupees, centimeter, etc.). Also, solve it.
Find the value of k for which the quadratic equation kx (x − 2) + 6 = 0 has two equal roots.
The ratio of fruit trees and vegetable trees in an orchard is 3:4. If 6 more trees of each type are planted, the ratio of trees would be 6:7. Find the number of fruit trees and vegetable trees in the orchard.
The ratio of fruit trees and vegetable trees = 3:4
So, let the number of fruit trees= 3x and the number of vegetable trees = `square`
From the given condition,
`(3x + square)/(square + square) = square/square`
`square (3x + square) = square (square + square)`
`square + square = square + square`
`square - square = square - square`
`- square = - square`
`square = square`
x = `square`
∴ Number of fruit trees in the orchard = 3x = 3 × `square` = `square` and number of vegetable trees in the orchard = 4x = 4 × `square` = `square`
Hence, the number of fruit trees and vegetable trees in the orchard are `square` and `square` respectively.

In the adjoining fig. `square` ABCD is a trapezium AB || CD and its area is 33 cm2. From the information given in the figure find the lengths of all sides of the `square` ABCD. Fill in the empty boxes to get the solution.
Solution: `square` ABCD is a trapezium.
AB || CD
`"A"(square "ABCD") = 1/2 ("AB" + "CD") xx`______
33 = `1/2 ("x" + 2"x" + 1) xx `______
∴ ______ = (3x + 1) × ______
∴ 3x2 +______ − ______ = 0
∴ 3x(______) + 10(______) = 0
∴ (3x + 10) (______) = 0
∴ (3x + 10) = 0 or ______ = 0
∴ x = `-10/3` or x = ______
But length is never negative.
∴ `"x" ≠ -10/3`
∴ x = ______
AB = ______, CD = ______, AD = BC = ______
