Advertisements
Advertisements
प्रश्न
Construct a word problem on quadratic equation, such that one of its answers is 20 (years, rupees, centimeter, etc.). Also, solve it.
उत्तर
Find the roots of a equation x² - 10x = 200
x² - 10x = 200
=> x² - 10x - 200 = 0
=> x² - 20x + 10x - 200 = 0
=> x(x - 20) + 10(x - 20) = 0
=> (x + 10)(x-20) = 0
=> x = 20 or x = -10
hence one of its answer is 20
APPEARS IN
संबंधित प्रश्न
The divisor and quotient of the number 6123 are same and the remainder is half the divisor. Find the divisor.
The roots of a quadratic equation are 5 and -2. Then, the equation is
(a)`x^2-3x+10=0` (b)`x^2-3x-10=0` (c)x^2+3x-10=0 (d)`x^2+3x+10=0`
The roots of `ax^2+bx+c=0`,a≠0 are real and unequal, if `(b^2-4ac)` is
(a)>0 (b)=0 (c)<0 (d)none of these
The roots of the quadratic equation `2x^2-x-6=0`
(a)`-2, 3/2` (b) `2, -3/2`
(c)` -2, 3/2` (d) `2, 3/2`
Find the roots of the quadratic equation `2x^2-x-6=0`
If 1 is a root of the equations ay2 + ay + 3 = 0 and y2 + y + b = 0 then ab equals: ?
Solve for x: `3x^2-2sqrt6x+2=0`
Decide whether the following equation is quadratic equation or not.
(m + 2) (m – 5) = 0
Write the following equation in the form ax2 + bx + c= 0, then write the values of a, b, c for the equation.
x2 – 9 = 13
Suyash scored 10 marks more in second test than that in the first. 5 times the score of the second test is the same as square of the score in the first test. Find his score in the first test.
Pratik takes 8 hours to travel 36 km downstream and return to the same spot. The speed of boat in still water is 12 km. per hour. Find the speed of water current.
Choose the correct answer for the following question.
The roots of x2 + kx + k = 0 are real and equal, find k.
Which of the following is a quadratic equation ?
If in an A. P., d = 10, find t6 - t2.
Write the degree of Polynomial 5x2 + 2x + 3x4 + 4.
Complete the following activity to form a quadratic equation.
Activity:
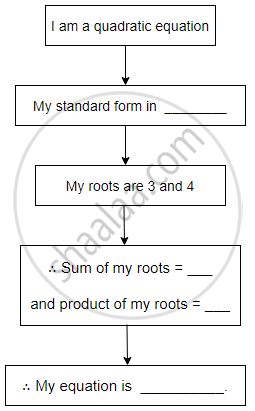
If 460 is divided by a natural number, then quotient is 2 more than nine times the divisor and remainder is 5. Find the quotient and divisor.
The ratio of fruit trees and vegetable trees in an orchard is 3:4. If 6 more trees of each type are planted, the ratio of trees would be 6:7. Find the number of fruit trees and vegetable trees in the orchard.
The ratio of fruit trees and vegetable trees = 3:4
So, let the number of fruit trees= 3x and the number of vegetable trees = `square`
From the given condition,
`(3x + square)/(square + square) = square/square`
`square (3x + square) = square (square + square)`
`square + square = square + square`
`square - square = square - square`
`- square = - square`
`square = square`
x = `square`
∴ Number of fruit trees in the orchard = 3x = 3 × `square` = `square` and number of vegetable trees in the orchard = 4x = 4 × `square` = `square`
Hence, the number of fruit trees and vegetable trees in the orchard are `square` and `square` respectively.
