Advertisements
Advertisements
प्रश्न
The sum of three consecutive natural numbers is 114. Find the numbers.
उत्तर
Let the three consecutive natural numbers be x, (x+1), (x+2).
According to the question:
x + (x + 1) + (x + 2) = 114
or, x + x + 1 + x + 2 = 114
or, 3x + 3 = 114
or, 3x + 3 − 3 = 114 − 3 [Subtracting 3 from both the sides]
or, 3x = 111
or, `(3x)/3=111/3` [Dividing both the sides by 3]
or, x = 37
Required numbers are:
x = 37
or, x + 1 = 37 + 1 = 38
or ,x + 2 = 37 + 2 = 39
Thus, the required numbers are 37, 38 and 39.
APPEARS IN
संबंधित प्रश्न
Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.
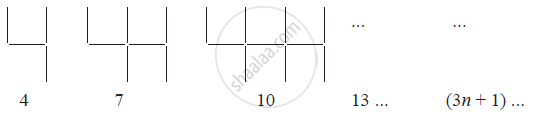
If the number of digits formed is taken to be n, the number of segments required to form n digits is given by the algebraic expression appearing on the right of each pattern.
How many segments are required to form 5, 10, 100 digits of the kind −

Use the given algebraic expression to complete the table of number patterns.
| S. No |
Expression |
Terms | |||||||||
| 1st | 2nd | 3rd | 4th | 5th | ... | 10th | ... | 100th | ... | ||
| 1 | 2n - 1 | 1 | 3 | 5 | 7 | 9 | - | 19 | - | - | - |
| 2 | 3n + 2 | 5 | 8 | 11 | 14 | - | - | - | - | - | - |
| 3 | 4n + 1 | 5 | 9 | 13 | 17 | - | - | - | - | - | - |
| 4 | 7n + 20 | 27 | 34 | 41 | 48 | - | - | - | - | - | - |
| 5 | n2 + 1 | 2 | 5 | 10 | 17 | - | - | - | - | 10001 | - |
If a number is tripled and the result is increased by 5, we get 50. Find the number.
The sum of two consecutive even numbers is 74. Find the numbers.
The area of a square having each side x is ______.
The additive inverse of an integer x is 2x.
A cube is a three-dimensional figure as shown in the given figure. It has six faces and all of them are identical squares. The length of an edge of the cube is given by l. Find the formula for the total length of the edges of a cube.

The sum of first n natural numbers is given by `1/2n^2 + 1/2n`. Find the sum of first 11 natural numbers.
If ![]() = 2x + 3,
= 2x + 3, ![]() = `3/2x + 7` and
= `3/2x + 7` and ![]() = x – 3 then find the value of:
= x – 3 then find the value of:
2![]() +
+ ![]() –
– ![]()
If ![]() = 2x + 3,
= 2x + 3, ![]() = `3/2x + 7` and
= `3/2x + 7` and ![]() = x – 3 then find the value of:
= x – 3 then find the value of:
`1/2`![]() +
+ ![]() – 3
– 3![]()
