Advertisements
Advertisements
प्रश्न
Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.
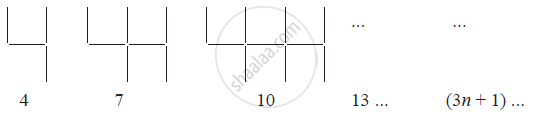
If the number of digits formed is taken to be n, the number of segments required to form n digits is given by the algebraic expression appearing on the right of each pattern.
How many segments are required to form 5, 10, 100 digits of the kind −

उत्तर
It is given that the number of segments required to form n digits of the kind

is is (3n + 1)
Number of segments required to form 5 digits = (3 × 5 + 1)
= 15 + 1 = 16
Number of segments required to form 10 digits = (3 × 10 + 1)
= 30 + 1 = 31
Number of segments required to form 100 digits = (3 × 100 + 1)
= 300 + 1 = 301
APPEARS IN
संबंधित प्रश्न
Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.
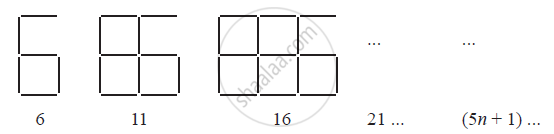
If the number of digits formed is taken to be n, the number of segments required to
form n digits is given by the algebraic expression appearing on the right of each pattern.
How many segments are required to form 5, 10, 100 digits of the kind −
Write down the following in the product form: x2y4
Write down the following in the product form: 6y5
If 11 is subtracted from 4 times a number, the result is 89. Find the number.
The sum of three consecutive natural numbers is 114. Find the numbers.
If a number is tripled and the result is increased by 5, we get 50. Find the number.
Reena is 6 years older than her brother Ajay. If the sum of their ages is 28 years, what are their present ages?
A man is 4 times as old as his son. After 16 years he will be only twice as old as his son. Find their present ages.
A man is thrice as old as his son. Five years ago the man was four times as old as his son. Find their present ages.
The side of an equilateral triangle is shown by l. Express the perimeter of the equilateral triangle using l.
To find sum of three numbers 14, 27 and 13, we can have two ways:
- We may first add 14 and 27 to get 41 and then add 13 to it to get the total sum 54 or
- We may add 27 and 13 to get 40 and then add 14 to get the sum 54. Thus, (14 + 27) + 13 = 14 + (27 + 13)
This can be done for any three numbers. This property is known as the associativity of addition of numbers. Express this property which we have already studied in the chapter on whole numbers, in a general way, by using variables a, b and c.
The expression for the number of diagonals that we can make from one vertex of a n sided polygon is ______.
The speed of car is 55 km/hrs. The distance covered in y hours is ______.
A wire is (7x – 3) metres long. A length of (3x – 4) metres is cut for use. Now, answer the following questions:
- How much wire is left?
- If this left out wire is used for making an equilateral triangle. What is the length of each side of the triangle so formed?
The sum of first n natural numbers is given by `1/2n^2 + 1/2n`. Find the sum of first 11 natural numbers.
The sum of squares of first n natural numbers is given by `1/6n(n + 1)(2n + 1)` or `1/6(2n^3 + 3n^2 + n)`. Find the sum of squares of the first 10 natural numbers.
If ![]() = `3/4x - 2` and
= `3/4x - 2` and ![]() = x + 6, then find the value of:
= x + 6, then find the value of:
![]() –
– ![]()
Write an expression for the sum of 1 and twice a number n. If you let n be any odd number, will the result always be an odd number?
