Advertisements
Advertisements
प्रश्न
The three rods shown in figure have identical geometrical dimensions. Heat flows from the hot end at a rate of 40 W in the arrangement (a). Find the rates of heat flow when the rods are joined as in arrangement (b) and in (c). Thermal condcutivities of aluminium and copper are 200 W m−1°C−1 and 400 W m−1°C−1 respectively.

उत्तर
For arrangement (a),
Temperature of the hot end ,T1 = 100°C
Temperature of the cold end ,T2 = 0°C
`R_s = R_1 + R_2 + R_3`
`(l)/(K_{AI}A) + l/(K_{cu}A) + {l}/(K_{Al}A)`
`(l)/(A) ( 1/200 +1/400 + 1/200)`
`1/A (5/400)`
`1/Axx 1/80`
`(dQ)/d = q = Rate of flow of heat = (T_1 - T_2)/R_s `
`= (100 - 0)/((1/Axx1/(80))`
Given :
q = 40W
`40 = (100)/(1/Axx 1/80)`
`⇒ l/A = 200`
`⇒ l/A = 1/200 `
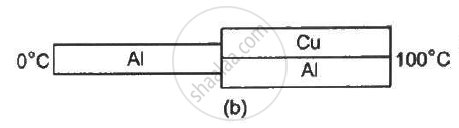
For arrangement (b),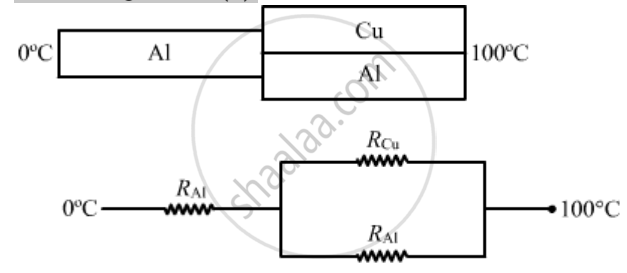
`"R_net" = R_[AI} + (R_cuxxR_{AI})/(R_cu = R_{AI)}`
`= l / (K_AI A) + (l/(K_cuA)xxl/K_(AI))/(l / (K_{cu}A9 )+ (l)/ (K_{AL}A)`
`= (l)/(A.K_Al) +( l )/ (A(K_AL + K_cu)) `
`= l/A (1/200 + 1/"200 + 400")`
`=l/A ( 1/200 + 1/600)`
= `4/600 1/A`
Rate of flow of heat is given by
`q = (T_1 - T_2)/ R_"net"`
`= ((100 - 0))/ (4 l) 600 A`
`= (100xx600)/4 xx1/200`
= 75 W
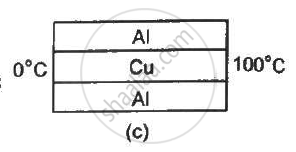
For arrangement (c),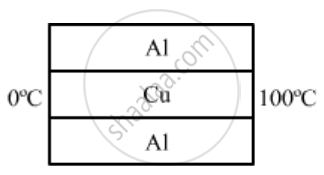
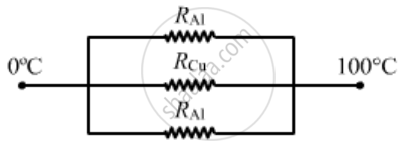
`1 / (R"net") = (1)/(R_{AI)) + 1/R_(cu)+ 1/(R_AI) `
`= K_{K_{AI}}/ (l)+ K_(cuA)/l + (K_{Al}A)/l`
`1/R_"net" = (K_Al + K_( cu) + K_(Al))A/l`
`l /R_"(net)" = (200 + 400 +200)`
`1/ R_"net" = 200/800`
`=(100)/(1/4)`
rate of heat flow = `(DeltaT)/R_"net"`
`= 100/1/4`400 W
APPEARS IN
संबंधित प्रश्न
A bullet of mass 20 g enters into a fixed wooden block with a speed of 40 m s−1 and stops in it. Find the change in internal energy during the process.
A brick weighing 4.0 kg is dropped into a 1.0 m deep river from a height of 2.0 m. Assuming that 80% of the gravitational potential energy is finally converted into thermal energy, find this thermal energy is calorie.
A van of mass 1500 kg travelling at a speed of 54 km h−1 is stopped in 10 s. Assuming that all the mechanical energy lost appears as thermal energy in the brake mechanism, find the average rate of production of thermal energy is cal s−1.
The blocks of masses 10 kg and 20 kg moving at speeds of 10 m s−1 and 20 m s−1respectively in opposite directions, approach each other and collide. If the collision is completely inelastic, find the thermal energy developed in the process.
One end of a metal rod is kept in a furnace. In steady state, the temperature of the rod
A hot liquid is kept in a big room. The logarithm of the numerical value of the temperature difference between the liquid and the room is plotted against time. The plot will be very nearly
A uniform slab of dimension 10 cm × 10 cm × 1 cm is kept between two heat reservoirs at temperatures 10°C and 90°C. The larger surface areas touch the reservoirs. The thermal conductivity of the material is 0.80 W m−1 °C−1. Find the amount of heat flowing through the slab per minute.
Water at 50°C is filled in a closed cylindrical vessel of height 10 cm and cross sectional area 10 cm2. The walls of the vessel are adiabatic but the flat parts are made of 1-mm thick aluminium (K = 200 J s−1 m−1°C−1). Assume that the outside temperature is 20°C. The density of water is 100 kg m−3, and the specific heat capacity of water = 4200 J k−1g °C−1. Estimate the time taken for the temperature of fall by 1.0 °C. Make any simplifying assumptions you need but specify them.
A metal rod of cross sectional area 1.0 cm2 is being heated at one end. At one time, the temperatures gradient is 5.0°C cm−1 at cross section A and is 2.5°C cm−1 at cross section B. Calculate the rate at which the temperature is increasing in the part AB of the rod. The heat capacity of the part AB = 0.40 J°C−1, thermal conductivity of the material of the rod = 200 W m−1°C−1. Neglect any loss of heat to the atmosphere
A hole of radius r1 is made centrally in a uniform circular disc of thickness d and radius r2. The inner surface (a cylinder a length d and radius r1) is maintained at a temperature θ1 and the outer surface (a cylinder of length d and radius r2) is maintained at a temperature θ2 (θ1 > θ2). The thermal conductivity of the material of the disc is K. Calculate the heat flowing per unit time through the disc.
Figure (28-E2) shows a copper rod joined to a steel rod. The rods have equal length and equal cross sectional area. The free end of the copper rod is kept at 0°C and that of the steel rod is kept at 100°C. Find the temperature at the junction of the rods. Conductivity of copper = 390 W m−1°C−1 and that if steel = 46 W m−1°C−1.

An aluminium rod and a copper rod of equal length 1.0 m and cross-sectional area 1 cm2 are welded together as shown in the figure . One end is kept at a temperature of 20°C and the other at 60°C. Calculate the amount of heat taken out per second from the hot end. Thermal conductivity of aluminium = 200 W m−1°C−1 and of copper = 390 W m−1°C−1.

Following Figure shows an aluminium rod joined to a copper rod. Each of the rods has a length of 20 cm and area of cross section 0.20 cm2. The junction is maintained at a constant temperature 40°C and the two ends are maintained at 80°C. Calculate the amount of heat taken out from the cold junction in one minute after the steady state is reached. The conductivites are KAt = 200 W m−1°C−1 and KCu = 400 W m−1°C−1.

The two rods shown in following figure have identical geometrical dimensions. They are in contact with two heat baths at temperatures 100°C and 0°C. The temperature of the junction is 70°C. Find the temperature of the junction if the rods are interchanged.

Seven rods A, B, C, D, E, F and G are joined as shown in the figure. All the rods have equal cross-sectional area A and length l. The thermal conductivities of the rods are KA = KC = K0, KB = KD = 2K0, KE = 3K0, KF = 4K0 and KG = 5K0. The rod E is kept at a constant temperature T1 and the rod G is kept at a constant temperature T2 (T2 > T1). (a) Show that the rod F has a uniform temperature T = (T1 + 2T2)/3. (b) Find the rate of heat flowing from the source which maintains the temperature T2.
An amount n (in moles) of a monatomic gas at an initial temperature T0 is enclosed in a cylindrical vessel fitted with a light piston. The surrounding air has a temperature Ts (> T0) and the atmospheric pressure is Pα. Heat may be conducted between the surrounding and the gas through the bottom of the cylinder. The bottom has a surface area A, thickness x and thermal conductivity K. Assuming all changes to be slow, find the distance moved by the piston in time t.
A spherical ball of surface area 20 cm2 absorbs any radiation that falls on it. It is suspended in a closed box maintained at 57°C. (a) Find the amount of radiation falling on the ball per second. (b) Find the net rate of heat flow to or from the ball at an instant when its temperature is 200°C. Stefan constant = 6.0 × 10−8 W m−2 K−4.
