Advertisements
Advertisements
प्रश्न
The value of \[\frac{(0 . 013 )^3 + (0 . 007 )^3}{(0 . 013 )^2 - 0 . 013 \times 0 . 007 + (0 . 007 )^2}\] is
विकल्प
0.006
0.02
0.0091
0.00185
उत्तर
The given expression is
\[\frac{(0 . 013 )^3 + (0 . 007 )^3}{(0 . 013 )^2 - 0 . 013 \times 0 . 007 + (0 . 007 )^2}\]
Assume a = 0.013and b = 0.007. Then the given expression can be rewritten as
`(a^+b^3)/(a^2 - ab + b^2)`
Recall the formula for sum of two cubes
`a^3 +b^3 = (a+b )(a^2 - ab + b^2)`
Using the above formula, the expression becomes
`((a+b)(a^2 - ab + b^2))/(a^2 - ab + b^2)`
Note that both a and b are positive. So, neither `a^3 +b^3`nor any factor of it can be zero.
Therefore we can cancel the term `(a^2 - ab+b^2)`from both numerator and denominator. Then the expression becomes
`((a+b)(a^2 - ab + b^2))/(a^2 - ab + b^2) = a+b`
` = 0.013 + 0 .007`
` = 0.02`
APPEARS IN
संबंधित प्रश्न
Factorize `7(x - 2y)^2 - 25(x - 2y) + 12`
What are the possible expressions for the dimensions of the cuboid whose volume is 3x2 - 12x.
Evaluate: `(1/2 "a" + 1/2 "b") (1/2 "a" - 1/2 "b")`
Multiply: (2x - 3y)(2x - 3y)
Multiply: (2x + 5y + 6)(3x + y - 8)
Divide: 9x2 - 24xy + 16y2 by 3x- 4y
Write in the form of an algebraic expression:
Perimeter (P) of a rectangle is two times the sum of its length (l) and its breadth (b).
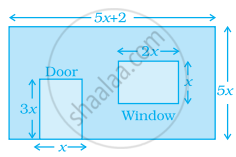
The figure shows the dimensions of a wall having a window and a door of a room. Write an algebraic expression for the area of the wall to be painted.
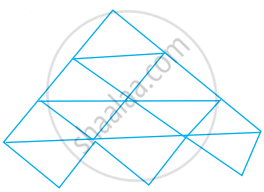
A triangle is made up of 2 red sticks and 1 blue sticks  . The length of a red stick is given by r and that of a blue stick is given by b. Using this information, write an expression for the total length of sticks in the pattern given below:
. The length of a red stick is given by r and that of a blue stick is given by b. Using this information, write an expression for the total length of sticks in the pattern given below:
Express the following properties with variables x, y and z.
Associative property of addition
