Advertisements
Advertisements
प्रश्न
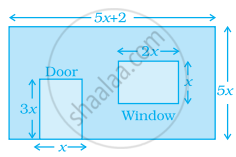
The figure shows the dimensions of a wall having a window and a door of a room. Write an algebraic expression for the area of the wall to be painted.
Advertisements
उत्तर
We have a wall of dimension 5x × (5x + 2) having a window and a door of dimension (2x × x) and (3x × x), respectively.
Then, area of the window = 2x × x = 2x2 sq.units
Area of the door = 3x × x = 3x2 sq.units
And area of wall = (5x + 2) × 5x = (25x2 + 10x) sq.units
Now, area of the required part of the wall to be painted
= Area of the wall – (Area of the window + Area of the door)
= 25x2 + 10x – (2x2 + 3x2)
= 25x2 + 10x – 5x2
= 20x2 + 10x
= 2 × 2 × 5 × x × x + 2 × 5 × x
= 2 × 5 × x(2x + 1)
= 10x(2x + 1) sq.units
APPEARS IN
संबंधित प्रश्न
Factorize x2 - y2 - 4xz + 4z2
Factorize 125x3 - 27 y3 - 225x2 y +135xy2
(3x - 2 y)3 + (2 y - 4z )3 + (4z - 3x)3
Find the value of the following expression: 81x2 + 16y2 − 72xy, when \[x = \frac{2}{3}\] and \[y = \frac{3}{4}\]
Write the number of the term of the following polynomial.
ax ÷ 4 – 7
Divide: 8x + 24 by 4
Write the coefficient of x2 and x in the following polynomials
`4 + 2/5x^2 - 3x`
In the formula, area of circle = πr2, the numerical constant of the expression πr2 is ______.
In the expression 2πr, the algebraic variable is ______.
Match Column I with Column II in the following:
| Column I | Column II |
| 1. The difference of 3 and a number squared | (a) 4 – 2x |
| 2. 5 less than twice a number squared | (b) n2 – 3 |
| 3. Five minus twice the square of a number | (c) 2n2 – 5 |
| 4. Four minus a number multiplied by 2 | (d) 5 – 2n2 |
| 5. Seven times the sum of a number and 1 | (e) 3 – n2 |
| 6. A number squared plus 6 | (f) 2(n + 6) |
| 7. 2 times the sum of a number and 6 | (g) 7(n + 1) |
| 8. Three less than the square of a number | (h) n2 + 6 |
